 obliczam pochodne funkcji f'(x) = (2x+2)*e−x −(x2+2x−1)*e−x
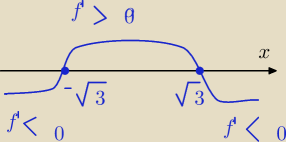
f'(x)=(3−x2)*e−x ; f'(x) >0 <=> 3−x2>0 <=> (√3−x)(√3+x)>0
na podstawie wykresu dla f'(x) otrzymuje ,że f'(x) >0 <=> x∊(−√3 ; √3 )
w tym przedziale funkcja jest rosnąca
obliczam drugą pochodną funkcji
f''(x) = −e−x*(3−x2) + e−x *(−2x) = e−x *(x2−2x−3)
f''(x) >0 <=> x2 −2x −3 >0 => x∊ (−∞ ;−1 )∪(3 ;∞) funkcja jest wypukła
część wspólna tych przedziałów to x ∊( −√3 ;−1)
obliczam pochodne funkcji f'(x) = (2x+2)*e−x −(x2+2x−1)*e−x
f'(x)=(3−x2)*e−x ; f'(x) >0 <=> 3−x2>0 <=> (√3−x)(√3+x)>0
na podstawie wykresu dla f'(x) otrzymuje ,że f'(x) >0 <=> x∊(−√3 ; √3 )
w tym przedziale funkcja jest rosnąca
obliczam drugą pochodną funkcji
f''(x) = −e−x*(3−x2) + e−x *(−2x) = e−x *(x2−2x−3)
f''(x) >0 <=> x2 −2x −3 >0 => x∊ (−∞ ;−1 )∪(3 ;∞) funkcja jest wypukła
część wspólna tych przedziałów to x ∊( −√3 ;−1)
