objętość Ania: Oblicz objętość brył ograniczonych powierzchniami: y=2, y=x², z=1, z=y+x

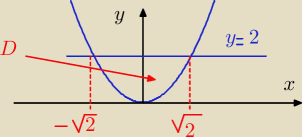
Leszek: V= ∫ ∫ [y+x−1]dxdy D: x∊ <−√2 ; √2 > i y∊ < x², 2 > D V= ∫ dx ∫ [y + x −1]dy = ∫ dx [ 0,5y² +xy −y] i po podstawieniu y z podanego przedziału otrzymujemy V = ∫ dx[(2+2x−2)−(0,5x⁴−x³−x²)]= ∫ dx[−0,5x⁴ +x³ +x²+2x]= = .... to już jest całka z funkcji elementarnych , proszę wykonać obliczenia