pochodne nice: Móglby ktoś podpowiedzieć jak się zabrać? 1.Dobrać parametry p, q tak, aby funkcja f(x) = e^x+x dla x < 0, x²+px+q dla 0 < x miała pochodną w punkcie x0 = 0. Narysować wykres otrzymanej funkcji

Jerzy: Gdzie jest nierownosc slaba ?

nice: Nie rozumiem

Jerzy: Musi byc: p = 0 q = 1 i glowkuj dlaczego

Jerzy: Zle opisalas/es przedzialy

Qulka: mi wyszło p=2

nice: e² dla x (tutaj powinno być mniejsze, równe 0) nie wiem jak to zaznaczyć

Jerzy: to w końcu jaka jest ta funkcja ? e² + x , czy : e^x + x dla x → 0⁻ granica wynosi 1 zatem trójmiam musi mieć postać: x² + 1 , bo wtedy granica x → 0⁺ = 1 i funkcja jest ciagła

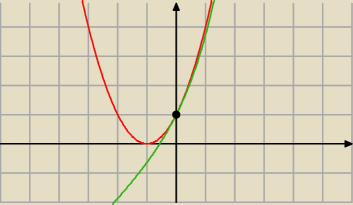
g: Po pierwsze trzeba uzupełnić funkcję f(x) o punkt f(0) = lim(x→0⁻)(e^x+x) = 1. Przyda się jeszcze granica pochodnej lim(x→0⁻)(e^x+x)' = 2 Teraz od tej postaci zależnej od p,q zażądamy, żeby przy x→0⁺ miała granice: f(x) = x²+px+q → q = 1 f'(x) = 2x+p → p = 2

Qulka: nad okienkiem wpisywania jest taki przycisk ≤