maksima, minima matematyk1: Niech funkcja w:R R−>R będzie zadana wzorem w(x) = 2x⁴ − 3x² + 1 a) wyznacz lokalne minima i maksima funkcji w b) przedziały w których funkcja w rośnie i przedziały w których funkcja w maleje c) przedziały w których funkcja w jest wypukła i przedziały w których funkcja w jest wklęsła

matematyk1: a) zacząłem od wyznaczenia pochodnej funkcji w i wyszło mi 8x³ − 6x=0 ( przyrównuje do 0, bo wartość pochodnej w ekstremum jest =0 ) i tu mam ścianę

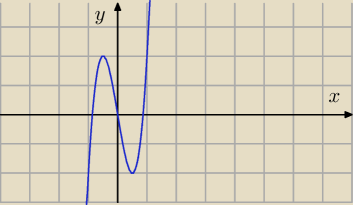
Leszek: w'(x) = 8x³ −6x =0 <=> 2x(4x²−3)=0 <=> 2x(2x−√3)(2x+√3) =0 punkty przegięcia funkcji w''(x) =0 <=> 24x²−6=0 <=> 6(2x−1)(2x+1)=0 wykres przedstawia y = w'(x) na jego podstawie można odczytać przedziały monotoniczności funkcji w(x)

matematyk1: czyli dla punktu a) − obliczam maksimum i minimum dla wartości −√3/4 i dla √3/4 podstawiając pod pierwotną funkcje?

matematyk1: i dla 0

Leszek: podstaw do funkcji w(x) wartości x=√3/2 i x=−√3/2 i x=0 a dla punktów przegięcia x=1/2 i x=−1/2

matematyk1: dla funkcji w: kolejno 5/8, 5/8 i 1

Mila: 1) Miejsca zerowe pochodnej: 8x³−6x=0 x(8x²−6)=0 x=0 lub 8x²−6=0 /:8

	√3		√3
x=0 lub x=		lub x=−
	2		2

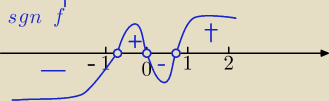
2) znak pochodnej, monotoniczność: x*(8x²−6)>0

	√3		√3
x*8*(x−		)*(x+		)>0
	2		2

	√3		√3
x∊(−		,0) ∪(		,∞)
	2		2

	√3		√3
f(x)↑ dla x∊(−		,0) ∪(		,∞)
	2		2

	√3		√3
f(x)↓ dla x∊(−∞,−		)∪(0,		)
	2		2

3) Ekstrema :

	√3		√3		1
Dla x=−		min. lokalne f(−		)=−
	2		2		8

Dla x=0 maks. lokalne f(0)=1

	√3		√3		1
Dla x=		min. lokalne f(		)=−
	2		2		8

matematyk1: racja mój błąd jest −1/8

matematyk1: a jak by się wykres zmienił gdyby przed funkcją był −?

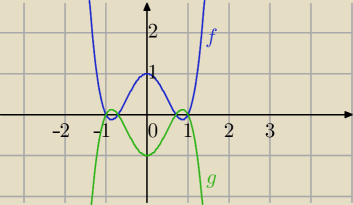
Mila: f(x) = 2x⁴ − 3x² + 1 g(x)=−f(x) wykres: −f(x) jest symetryczny względem OX do wykresu funkcji f(x).

matematyk1: punktem jedynym przegięcia będzie punkt 5/16?

matematyk1: 3/8

Mila: 22:09 masz napisane .