Pochodna funkcji
edta191: Cześć, mógłby mi ktoś wyjaśnić czy tak czy nie i dlaczego?
Pochodna f'(x
0) jest równa 0, gdy funkcja f ma maksimum w punkcie x
0.
Z góry dziękuję.

21 cze 18:54
edta191: Bardzo proszę o szybką pomoc.

21 cze 19:25
Mila:
Może mieć minimum albo maksimum, jeżeli przy przejściu przez x0 zmienia znak.
21 cze 19:52
edta191: Czyli konkretnie tak, czy jednak nie?
Bo mam wątpliwość co do prawdziwości tego zdania.
21 cze 19:58
jc: Jeśli f ma maximum (lokalne) w punkcie x0, jest określona w pewnym otoczeniu x0 oraz
jest różniczkowalna w x0, to f'(x0) = 0.
f(x0+ h) − f(x0) ≤ 0 dla małych h
[f(x0+ h) − f(x0) ] / h ≤ 0 dla h >0 ⇒ f'(x0) ≤ 0
[f(x0+ h) − f(x0) ] / h ≥ 0 dla h <0 ⇒ f'(x0) ≥ 0
⇒ f'(x0) = 0
21 cze 20:06
Leszek:
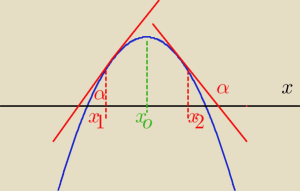
popatrz na interpretacje geometryczną pochodnej
f'
x1 >0 bo tg α >0 ; f'
x2 <0 bo tgα<0
f'
xo =0 dla x
o f
max(x
o)
dokładne rysunki i wyjaśnienia są w każdym podręczniku do analizy matematycznej
tego szukaj
21 cze 20:10
Mila:
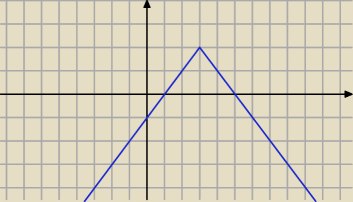
Funkcja może mieć maksimum w punkcie x
0 a pochodna nie istnieje.
21 cze 20:33
edta191: Dziękuję, zamąciła mi implikacja odwrotna.

21 cze 20:58
Leszek: zgadzam się , taka sama sytuacja jest w przypadku funkcji ciągłej f(x) = |x|
ale w pytaniu było że pochodna istnieje , dlatego tak graficznie to przedstawiłem.
Element pamięci wzrokowej w nauczaniu analizy matematycznej ( np. wykresy funkcji)
ma istotne znaczenie tak mi się wydaje .
21 cze 21:04


 popatrz na interpretacje geometryczną pochodnej
f'x1 >0 bo tg α >0 ; f'x2 <0 bo tgα<0
f'xo =0 dla xo fmax(xo)
dokładne rysunki i wyjaśnienia są w każdym podręczniku do analizy matematycznej
tego szukaj
popatrz na interpretacje geometryczną pochodnej
f'x1 >0 bo tg α >0 ; f'x2 <0 bo tgα<0
f'xo =0 dla xo fmax(xo)
dokładne rysunki i wyjaśnienia są w każdym podręczniku do analizy matematycznej
tego szukaj
 Funkcja może mieć maksimum w punkcie x0 a pochodna nie istnieje.
Funkcja może mieć maksimum w punkcie x0 a pochodna nie istnieje.
