dziedzina log:) Michał: dziedzina.. f(x)= √log_1/2x − log_1/2(x−1) + 1 log_1/2x − log_1/2(x−1) + 1>0 x>0 /\ x> 1 x∊(1, +∞) log_1/2x − log_1/2(x−1)>log_1/22

x
	− 2>0
x−1

po przekształceniach wyjdzie (−x−2)(x−1)>0 x<−2 /\ x>1 rozwiązanie to ⇒ x∊(1, +∞) dobrze ?

Anna: pomagam

Michał: oki

Michał: czy ktoś może sprawdzic?....

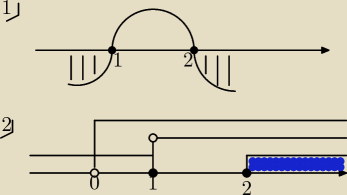Anna: 1) x > 0 2) x−1 > 0 ⇒ x > 1 3) log_1/2x − log_1/2(x−1) + 1 ≥ 0

	x		1
log1\2		+ log1\2		≥ 0
	x−1		2

	x
log1\2		≥ 0
	2(x−1)

	x
log1\2		≥ log1\21
	2(x−1)

	x
		≤ 1
	2(x−1)

	x
		− 1 ≤ 0
	2(x−1)

	x − 2(x−1)
		≤ 0
	2(x−1)

	x − 2x + 2
		≤ 0
	2(x−1)

2(2 − x)(x − 1) ≤ 0 I I x=2 x=1 Z rys. 1: x∊ ( −∞, 1 > ∪ < 2, ∞ ) Po złożeniu warunków − rys. 2 − mamy: D = < 2, ∞ )

Michał: Dziękuję bardzo

Anna:

Ada: log x2 > 1

5-latek: Zapis jest dla mnie niejasny