elektrostatyka Leszek: dany jest cienki pręt o długości L naładowany ładunkiem q . Wyznaczyć natężenie pola elektrostatycznego E na osi symetrii środkowej pręta w odległości x od jego środka .

jc: A jak naładowny jest pręt? jednorodnie, czy to może to metalowy pręt i ładunki się jakoś same rozłożyły?

Leszek: pret jest naladowany jednorodnie ( o stalej gestosci liniowej )

jc:

	x ds		2kq
E = (q/L) k ∫−L/2L/2		=
	(s2+x2)3/2		x √L2+4x2

jc: Można jeszcze wykonać rachunek dla punktu leżącego na prostej zawierającej odcinek. x < L/2, działa tylko fragment, dla x > L/2 dziala całość.

Leszek: Brak objasnien ,prosze pokazac jak obliczyc calke,przydalby sie schematyczny rysunek

jc: Co to jest oś symetrii środkowej?

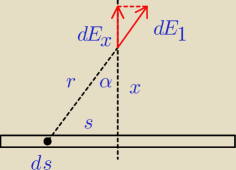
Leszek: na podstawie prawa Coulomba:

	kdq
dE1=
	r2

Leszek: SORRY puściłem za szybko

	kdq		q		xdα
dE1=		oraz dq =		*ds i s=x*tgα => ds =
	r2		L		cos2x

	kqxdα		kqdα		x
dE1=		=		ponieważ r=
	Lr2 cos2α		Lx		cosα

ale dE_x = cosα *dE₁ α_o

	kqcosα		2kq
to dEx =		*dα => Ex=		* ∫ cosα dα
	Lx		Lx

0

	2kq		L
czyli Ex=		*sinαo oraz sinαo =
	Lx		(2*√x2+0,25L2)

	2kq
zatem Ex =
	(x*√4x2 +L2)

jc: Tak właśnie policzyłem. Poziome składowe znoszą się.

	k dq		x
dq = (q/L) ds, dEx =		*
	r2		r

Drugi czynnik bierze się stąd, że patrzymy na składową pionową. Alternatywne rozwiązanie.

	qk		ds
Liczymy potencjał V(x) =		∫−L/2L/2
	L		√x2+s2

a potem różniczkujemy względem x (stawiamy minus przed wszystkim).

jc: Tak samo liczyłem

Leszek: OK , dzięki , z potencjału często łatwiej jest policzyć

	dV
E = −
	dx