 2.95 Z prostokątnego arkusza tektury o wymiarach 20cm x 30cm wycięto w rogach kwadraty o boku
długości x cm. Następnie po zgięciu powstałych brzegów zbudowano prostopadłościenne (otwarte)
pudełko.
a) Wyznacz wzór funkcji opisującej pole powierzchni bocznej tego pudełka w zależności od
długości boku wyciętego kwadratu; podaj dziedzinę tej funkcji.
b) Dla jakiej długości x polke powierzchni bocznej pudełka jest największa z możliwych? Wyznacz
to pole.
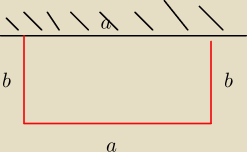
2.99 Gospodarz chcę siatką o długości 12 m wygrodzić na podwórku prostokątny dla psa
przylegający jednym bokiem do budynku. Jakie wymiary powinien mieć ten wybieg, aby jego pole
było jak największe? Oblicz jego powierzchnię.
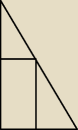
2.100 Z kawałka płótna w kształcie trójkąta prostokątnego o przyprostokątnych długości 40 cm i
30 cm hafciarka chce wyciąć prostokątną serwetkę w sposób podobny na rysunku (tym u góry).
Jakie powinny być wymiary serrwetki, żeby jej pole było jak największe?
2.95 Z prostokątnego arkusza tektury o wymiarach 20cm x 30cm wycięto w rogach kwadraty o boku
długości x cm. Następnie po zgięciu powstałych brzegów zbudowano prostopadłościenne (otwarte)
pudełko.
a) Wyznacz wzór funkcji opisującej pole powierzchni bocznej tego pudełka w zależności od
długości boku wyciętego kwadratu; podaj dziedzinę tej funkcji.
b) Dla jakiej długości x polke powierzchni bocznej pudełka jest największa z możliwych? Wyznacz
to pole.
2.99 Gospodarz chcę siatką o długości 12 m wygrodzić na podwórku prostokątny dla psa
przylegający jednym bokiem do budynku. Jakie wymiary powinien mieć ten wybieg, aby jego pole
było jak największe? Oblicz jego powierzchnię.
2.100 Z kawałka płótna w kształcie trójkąta prostokątnego o przyprostokątnych długości 40 cm i
30 cm hafciarka chce wyciąć prostokątną serwetkę w sposób podobny na rysunku (tym u góry).
Jakie powinny być wymiary serrwetki, żeby jej pole było jak największe?
 Np 2.99
2b+a=12
a= 12−2b
Pole prostokąta to a*b
(12−2b)*b= 12b−2b2 = −2b2+12b
Szukasz max tej funkcji (jest w wierzchołku
Np 2.99
2b+a=12
a= 12−2b
Pole prostokąta to a*b
(12−2b)*b= 12b−2b2 = −2b2+12b
Szukasz max tej funkcji (jest w wierzchołku
| −12 | ||
xbmax= | = 3 | |
| −4 |