ILOCZYNOWA -> KANONICZNA Zagrożony: 2.51 Dany jest wykres funkcji f w postaci iloczynowej. Podaj wzór f w postaci kanonicznej. Zadanie rozwiąż dwoma metodami; 1) Doprowadź wzór funkcji do piostaci ogólnej, a hnastępnie do kanonicznej. 2) Wyznacz wrównanie osi symetrii wykresu funkcji oraz wspólrzędne wierzchołka paraboli. a) f(x)=(x−1)(x+5) e) f(x)=3/5(x−1)(X+5).

6-latek : https://matematykaszkolna.pl/strona/3413.html Masz tu wszystko co potrzeba

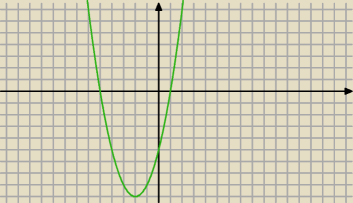
===: a) f(x)=(x−1)(x+5) Postać ogólną otrzymasz mnożąc czyli: f(x)=x²+5x−x−5 f(x)=x²+4x−5 Kanoniczną otrzymasz: "zwijając" do kwadratu sumy czyli f(x)=x²+4x+4−4−5 f(x)=(x+2)²−9 Drugi sposób to

	1−5
xw=		=−2 ... i to jest Twoje p
	2

f(x_w)=f(−2)=4−8−5=−9 ... i to jest Twoje q i kanoniczna f(x)=a(x−p)²+q ⇒ f(x)=(x+2)²−9