OGÓLNEJ I KANONICZNEJ Zagrożony: 2.39 Ile jest takich funkcji kwadratowych, których zbiorem wartości jest przedział <−4; +nieskończoność), wyróżnik równy 16, a wykres przecina oś OY w punkcie A(0, 5)>? wYZNACZ WYKRESY TYCH FUNKCJI W POSTACI OGÓLNEJ I KANONICZNEJ.

6-latek : Pytanie Co wiesz z wiadomosci ze zbiorem wartości funkcji jest przedziak <−4,∞) Jakie będzie wspolczynnik a? (−4) to jest najwieksza czy najmniejsza wartość tej funkcji ?

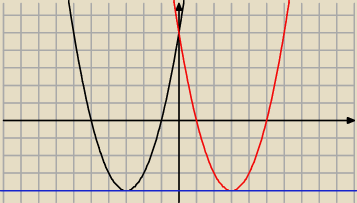
piotr1973: wykres przecina oś OY w punkcie A(0, 5) ⇒ c=5 zbiorem wartości jest przedział <−4;+nieskończoność) ⇒ a>0 q=−4 2*a*p+b=0, a*p²+b*p+5=−4, −b/a=2*p⇒(a=1, b=−6, p=3)∨(a=1, b=6, p=−3) czyli dwie funkcje: f(x)=x²−6x+5 = (x−3)²−4 (a=1, b=−6, c=5, p=3, q=−4) g(x)=x²+6x+5 = (x+3)²−4 (a=1, b=6, c=5, p=−3, q=−4)

piotr1973:

piotr1973: poprawka: zamiast trzeciego równania: −b/a=2*p ma być b²−20a=16, wyniki dobre