funkcja kwadratowa f w postaci kanonicznej Zagrożony: 2.23 Wyznacz wzór funkcji kwadratowej f w postaci kanonicznej, wiedząc, że dla argumentu 2 funkcja przyjmuje wartość najmniejszą, równą −3, a do jej wykresu należy punkt A(4,−1).) 2.24 Wyznacz wzór funkcji kwadratowej f w postaci kanonicznej, wiedząc, że dla argumentu −5 funkcja przyjmuje wartość największą, równą −8, a do jej wykresu należy punkt A(−3, −9). 2.25 Wyznacz wzór funkcji kwadratowej f w postaci kanonicznej, wiedząc, żezbiór wartości funkcji jest przedziałem (−nieskończonośc; 18>, a wartość 10 funkcja przyjmuje dla dwóch argumentów: 3 i −1.

===: ... jak widzę koleżka jest na rozszerzonej ... i zagrożony

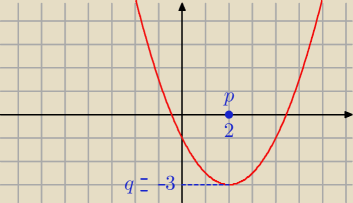
Janek191: 2.23 f(2) = q ⇒ p = 2 f(2) = − 3 więc f(x) = a*(x − p)² + q = a*( x − 2)² − 3 oraz A =( 4 , − 1) więc − 1 = a*( 4 − 2)² − 3 − 1 = 4 a − 3 4 a = 2 a = 0,5 Odp. f(x) = 0,5 *(x − 2)² − 3 ======================

Janek191: 2.24 rozwiązujemy analogicznie.

Janek191: 2.25 ZW = ( −∞ , 18 > ⇒ q = 18

	− 1+ 3
f(−1) = f(3) = 10 więc p =		= 1
	2

zatem f(x) = a*(x − p)² + q = a*(x − 1)² + 18 oraz f(3) = 10 10 = a*( 3 − 1)² + 18 10 = 4 a + 18 4 a = − 8 a = − 2 Odp. f(x) = − 2*( x − 1)² + 18 =====================