Zadanie
Wika: Witajcie i cieszcie sie tym o to zadaniem, a tak serio pomóżcie
Wyznacz wszystkie wartości parametru m, dla których równanie (x + 3) 2 = m + 1
ma dwa rozwiązania ujemne
Krok po kroku jak takie coś robić
15 cze 23:33
zef: x2+6x+9−m−1=0
x2+6x+8−m=0
a=1
b=6
c=8−m
I z Vieta:
x1x2>0
x1+x2<0
15 cze 23:34
zef: I oczywiście
Δ>0
Aby były 2 rozwiązania
15 cze 23:35
Wika: a co oznacza a , b i c ?
15 cze 23:40
zef: Postać ogólna funkcji kwadratowej:
ax2+bx+c=0
są to współczynniki przy zmiennej x2 x i stałej
Są one potrzebne aby dalej liczyć z vieta
15 cze 23:41
Wika: nie miałam jeszcze f. kwadratowej
15 cze 23:41
zef: To musisz graficznie..
Narysuj wykres (x+3)2, a m+1=k
k traktuj jako funkcję stałą i sprawdzaj po wykresie gdzie będą 2 rozwiązania ujemne. Tylko
dobrze oblicz miejsce przecięcia z Oy
15 cze 23:43
6-latek : Nie zartuj sobie
Wzory Vieta były a funkcji kwadratowej nie było ?
15 cze 23:43
Wika:
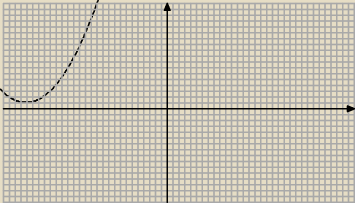
takie cos?
15 cze 23:45
zef:
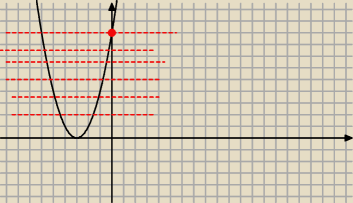
15 cze 23:45
Wika: wzorów tez nie mialam ;.;
15 cze 23:46
zef: I wyznacz miejsce przecięcia z osią Oy, kiedy to będziesz miała to wiesz że 2 rozwiązania
ujemne są od 0 do tego miejsca przecięcia.
m+1=k
k∊(0

o miejsca przecięcia z Oy)
k>0
k<miejsca przecięcia z Oy
wracamy z podstawieniem:
m+1>0
m+1<miejsca przecięcia z Oy
15 cze 23:47
Wika: troche skomplikowane to
15 cze 23:49
zef: miejsce przecięcia z osią Oy − miejsce gdzie x=0
(x+3)2
(0+3)2
9
m+1>0
m+1<9
Teraz obliczysz ?
15 cze 23:50
Wika: nw miejsce zerowe = − 3 ?
15 cze 23:53
zef: Wytłumaczyłem najlepiej jak potrafiłem, poddaję się. Poczytaj to co napisałem i popatrz na
rysunek
15 cze 23:54
Wika: zle?
16 cze 00:01
Wika: 
16 cze 00:07
Wika: a jutro sprawdzian
16 cze 00:07
16 cze 00:09
ICSP: (x + 3)2 = m + 1
Aby w ogóle mówić o istnieniu rozwiązań musi być : m + 1 ≥ 0.
Wtedy równanie można przekształcić do postaci:
(x + 3 + √m + 1)(x + 3 − √m + 1) = 0
skąd pierwiastki :
x1 = −3 − √m + 1
x2 = −3 + √m + 1
z czego x1 < x2 dla każdego m ≥ − 1
Wystarczy zatem aby x2 był pierwiastkiem ujemynm, więc dostajemy do rozwiazania nierówność:
x2 < 0
−3 + √m + 1 < 0
16 cze 00:12
 takie cos?
takie cos?

 o miejsca przecięcia z Oy)
k>0
k<miejsca przecięcia z Oy
wracamy z podstawieniem:
m+1>0
m+1<miejsca przecięcia z Oy
o miejsca przecięcia z Oy)
k>0
k<miejsca przecięcia z Oy
wracamy z podstawieniem:
m+1>0
m+1<miejsca przecięcia z Oy



