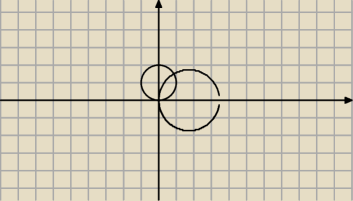
calka Benny: Obliczyć pole obszaru ograniczonego dwoma okręgami: x²−2√3x+y²=0 oraz x²+y²−2y=0 Jakoś na współrzędnych biegunowych to?

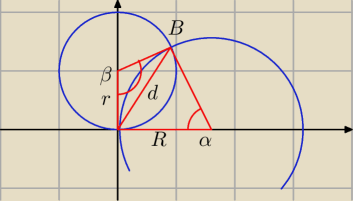
g: A może bez całkowania. Wyznaczyć punkt B, długość d, kąty α i β i pola dwóch kawałków. Ale pewnie trzeba całkować.

Benny: W poleceniu nie ma nic o całkach, ale lepiej będzie z

g: 1) Punkt przecięcia okręgów B: y = √3x, y²/3+y²−2y=0, y_B=3/2 (całkować będziemy po dy od 0 do y_B) 2) funkcje x(y) dla kół x_r(y) = √2y−y² x_R(y): Δ=12−4y², x_R(y)=√3−√3−y² 3) pole ∫₀^y_B (x_r(y) − x_R(y)) dy = ∫₀^3/2 (√2y−y² − √3 + √3−y²) dy

Benny: Dzięki w sumie udało mi się też to ogarnąć