Trygonometria, tgα i tgβ.
Ania:
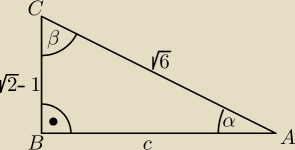
Witam. Mam problem z zadaniem z trygonometrii. Próbowałam już na dwa sposoby, jednak mijają się
one z prawidłowym wynikiem w książce. Liczę na waszą pomoc. Należy uwzględnić dane na rysunku
i obliczyć tgα i tgβ.
|CA| = √6 |CB| = √2 −1
15 cze 22:02
Jack:
z pitagorasa
|CA|
2 = |CB|
2 + |AB|
2
|AB|
2 = |CA|
2 − |CB|
2 = (
√6)
2 − (
√2−1)
2 = 6 − (2 − 2
√2 + 1) = 3 + 2
√2
|AB| =
√3+2√2 =
√2+1
zatem
15 cze 22:11
Bogdan:
c =
√2 + 1 (korzystamy z twierdzenia Pitagorasa)
15 cze 22:11
Ania: WYNIK W KSIĄŻCE: tgα=√3−2√2, tgβ=√3+2√2
MOJE ROZWIĄZANIE:
a
2+(√2−1)
2=(√6)
2
a
2 +2+1=6
a
2+3=6/−3
a
2=3
a=√3
Czy jest dobrze? Jak uzyskać wynik, taki jak w książce?
15 cze 22:12
Jack:
(√2−1)2 ≠ 2 + 1
popraw −>> skorzystaj ze wzoru skroconego mnozenia.
15 cze 22:15
Bogdan:
Ważny jest wynik poprawny, nieważne czy jest w książce, nie dopasowujemy wyniku
do odpowiedzi w książce.
| | √p2 − 1 | |
tgα = |
| = ... |
| | √2 + 1 | |
| | 1 | | √2 + 1 | |
tgβ = |
| = |
| = ... |
| | tgα | | √2 − 1 | |
15 cze 22:19
Ania: Dziękuję za pomoc i rady. Miłej nocy!
15 cze 22:23
aceton: z pitagorasa obliczasz 3 bok to będzie :
AB=x
x2=(√6)2 − (√2−1)2
x2=6−2+2√2−1
x2=2√2+3
x=√2+2√2+1
x=√(√2+1)2 = bezwzględna wartość z √2+1 ,a to jest równe √2+1
tgα= CB podzielone przez AB
tgβ to odwrotność tgα
15 cze 22:25