Oblicz objętość bryły V z całką podwójną Michał: Witam, może mi ktoś wytłumaczyć jak ruszyć z tym zadaniem? 0≤x≤1 1≤y≤2 0≤z≤x+y+1 Odpowiedź to 3

Leszek: V=∫∫(x+y+1)dxdy gdzie D to kwadrat x∊<0;1> i y∊<1;2> D 1 2 V= ∫ dx ∫ (x+y+1) dy = 3 ( to jest całkowanie elementarne) 0 1

Michał: Ok to rozumiem jak najbardziej z czego się wzięło lecz teraz mam do zrobienia trudniejszy przykład który jest inaczej zapisany

Michał: x²−4≤y≤−x²+2x+8 −5≤z≤x+y+4

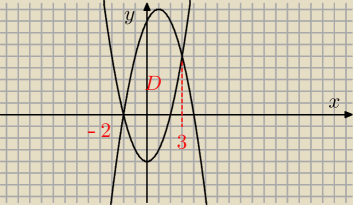
Leszek: ∫ ∫ (x+y−1)dxdy i całkuj D

Michał: Wszystko jasne dzięki