calka podwojna luki: Obliczyć całkę po obszarze D ⊂ R² ograniczonym liniami: ∫∫ (3x − y) dxdy, gdzie D: x = 0, y = 0, 2x + y = 2. D

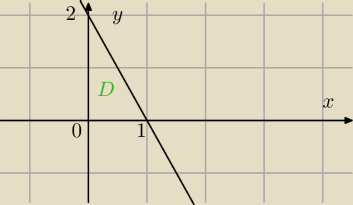
Leszek: obszar D: x∊<0;1> oraz y∊<0;2−2x²> 1 2−2x² 1 2−2x² ∫dx∫(3x−y)dy = ∫dx[3xy−0,5y²] 0 0 0 0

Leszek: przeskoczył mi kursor i puściłem za wcześnie ; ale dalej to już z górki ,

luki: dlaczego 2−2x²?

Leszek: zmienna y zmienia się od 0 do lini prostej o równaniu y=2−2x pomyłka w druku ( nie powinno być potęgi 2 )

luki: a skad sie wzielo 3xy−0,5y²? nie wiem w ogole jak sie rozwiazuje takie całki, stad moje pytanka i prosilbym o jakies jasniejsze wytlumaczenie

luki: czy wynik to będzie 1/3? Rozwiązałeś może to do końca? chcialbym sie upewnic

Leszek: TAK wynik masz poprawny 1/3 SORRY za błędy drukarskie

Leszek: Dla wprawy oblicz całkę po obszarze D⊂R² jeżeli D:x=0;y=0;x+2y−2=0 ∫∫(2x+y)dxdy D wynik : 5/3

H: Ok dzieki. Nie wiem za bardzo kiedy najpierw pisac dy a kiedy dx

Leszek: Poniewaz zmienna y zalezy od x ,to najpierw nalezy calkowac po y i dlatego piszemy ∫dx∫f(x,y)dy

H: Wyszlo mi 5 a nie 5/3 [2xy+1/2y²]1,0= 2x+1/2 (2x+1/2)dx=x²+1/2x [x²+1/2x]2,0=4+1?

Jerzy: A dlaczego po y liczysz w granicach [0,1] ?

H: 0,−1/2x+1?

Jerzy: Tak

H: Tak, wyszlo. Masz moze jeszcze jakis przykladzik?

H: Calka (3x+y)dxdy x=1 y=−3x y=3x

Jerzy: Wobec symetri obszaru względem osi OX wystarczy policzyć: ₀∫¹₀∫3x(3x+y)dxdy

Jerzy: 3x jest w górnej granicy drugiej całki

H: Wynik to 9/2?

Jerzy: To dopiero połowa

H: Co dalej?

Jerzy: wynik mnożysz przez 2 ( liczyliśmy tylko połowę całki )

H: Aha okej, ale nie rozumiem dlaczego mnozylismy tylko polowe calki i mam tez problem z wyznaczeniem granic obu calek (1,0 3x,0)

H: Dlaczego liczylismy*

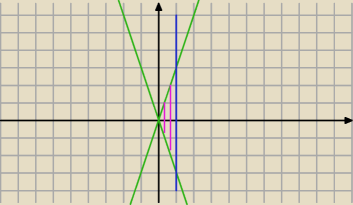
Jerzy: policzyliśmy tylko połowę fioletowego obszaru ( bo jest symetryczny wzgledem osi OX

H: Czyli rownie dobrze moglismy najpierw policzyc 1,0 −3x,0?

Jerzy: [0,1] [−3x,0] , albo po całości : [0,1] [−3x,3x]

H: Nie za bardzo lapie skad sie bierze ta kolejnosc...

Luki: Dlaczego raz jest 0,1 a raz 1,0