g:
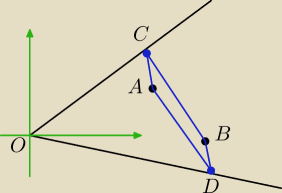
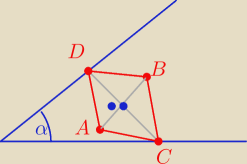
Elegancko było by konstrukcyjnie wyznaczyć punkty C i D, ale nie wiem jak.
Można próbować analitycznie.
Półproste sparametryzowane są wektorami kierunkowymi v=(v
x; v
y) i u=(u
x; u
y).
Celem jest znalezienie takich C=v*t
1 i D=u*t
2, które spełniają warunki zadania.
v i u są dane, więc trzeba znaleźć skalary t
1 i t
2.
Warunki w zapisie wektorowym:
|v*t
1 − A| = |u*t
2 − B| (równość długości)
(v*t
1 − A) x (v*t
2 − B) = 0 (równoległość)
Po rozpisaniu na współrzędne
(v
x*t
1−A
x)
2 + (v
y*t
1−A
y)
2 = (u
x*t
2−B
x)
2 + (u
y*t
2−B
y)
2
(v
x*t
1−A
x)*(u
y*t
2−B
y) − (v
y*t
1−A
y)*(u
x*t
2−B
x) = 0
Po wymnożeniu otrzymamy układ równań typu:
a
1t
12 +b
1t
1 + c
1 = a
2t
22 +b
2t
2 + c
2
dt
1t
2 + et
1 + ft
2 + g = 0
Teraz już tylko rozwiązać i znaleźć t
1 i t
2.
