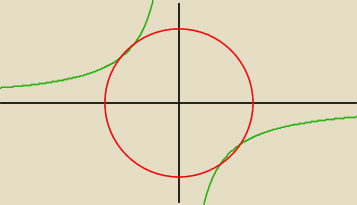
funkcja homograficzna Adam: Cześć mam funkcję homograficzną ^−a_x, jaka jest odległość tego 'przegięcia' funkcji od początku układu? inaczej − jak obliczyć promień okręgu?

ICSP:

	a2
f(x) = x2 +		, x > 0
	x2

Szukamy minimum funkcji f(x). Stosując nierównośc między średnią arytmetyczną oraz geometryczną mamy :

a2   x2 +   x2
	≥ √a2
2

Jeżeli założymy dodatkowo a > 0 to otrzymujemy : f(x) ≥ 2a. Stąd r = √2a

Adam: ICSP, dziękuję

Jerzy: Można też wyznaczyć punkt przecięcia hiperboli z prostą y = −x i obliczyć odległość tego punktu od poczatku układu współrzędnych