Analiza 2 - sprawdzenie Michał: Parę zadanek z Analizy 2: 1a)Wyznaczyć dziedzinę i ekstrema funkcji f(x,y)=2ln(xy)−y²−16x b)Znaleźć ekstrema warunkowe. Warunek xy−1=0 a)Dziedzina xy>0 ⇔ (x ⋀ y) > 0 ⋁ (x ⋀ y) < 0

	1		2
fx=2ln(xy)−y2−16x=2*		*(xy)`−16=		−16
	xy		x

	1		2
fy=2*		*(xy)`−2y=		−2y
	xy		y

2		1
	−16=0 ⇒ x=
x		8

2
	−2y=0 ⇒ y= 1 ⋁ −1 − (odrzucamy dziedzina)
y

	1
P(		;1)
	8

	2		2
fxx=		`−16=−
	x		x2

	2
fyy=−		−2
	y2

fxy=fyx=2 W=(−128*(−4))−2=510 > 0 fxx<0 W punkcie P funkcja f osiąga maksimum

Michał: b) z=2ln(xy)−y²−16x g(x,y)=xy−1=0 2ln(xy)−y²−16x+αxy−α

	2
fx=		−16+αy
	x

	2
fy=		−2y+αx
	y

fα=xy−1

2
	−16+αy=0
x

	2
fy=		−2y+αx=0
	y

fα=xy−1=0

	1
x=
	2

y=2 α=6

	1
P(		,2,6)
	2

gx=y gy=y

	2
fxx=−
	x2

	2
fyy=−		−2
	y2

fxy=fyx=α H=0+6+6+2−0+10=24>0 − W P osiąga maksimum Z_max=2ln1−2−8=−10

Michał:

	y
2. Niech f(x,y) = yln		oraz W(x,y)=x2yfxx+y2fyy
	x

a)Wyznacz dziedzinę i najprostszą postać W(x,y) b)Narysuj zbiór (x,y): W(x,y)>x+2 a)Dziedzina (y ⋀ x ) > 0 ⋁ (y ⋀ x ) < 0

	x		y		y
fx=y*		*(		)`=−
	y		x		x

	1		y
fxx=−y*		=
	x2		x2

	y		y		y
fy=y`*ln		+y*(ln		)`=ln		+1
	x		x		x

	1
fyy=
	y

	y		1
W(x,y)=x2y*		+y2*		=y2+y
	x2		y

y²+y>x+2

Michał: Teraz jak zaznaczyć ten zbiór?

Michał: Ktoś sprawdzi? Jakieś wskazówki?

Jerzy: f(y) = y² + y ... rysyjesz tak jak wykres f(x) = x² + x , tylko w obróconym o 90 stopni układzie współrzędnych potem y = x + 2 i zaznaczasz obszar, gdzie parabola ( leżąca) leży nad prostą

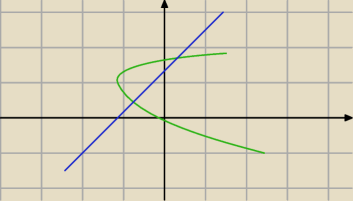
Jerzy: Mniej więcej coś takiego

Michał: Tak podejrzewałem. Dzięki! A te wcześniejsze zadania dobrze?