Parametry Stooley: 1.117 Naszkicuj wykres funkcji f(x)=|x+4|−|1−x|. Na podstawie wykresu: a)wyznacz parametr m dla którego rozwiązaniem równania f(x)=1−2m jest liczba −2 b) Wyznacz wszystkie wartości par. m dla których |x+4|−|1−x|=1−2m ma tylko 1 rozwiązanie. 1.119 Dane jest równanie z niewiadomą x: x²−4x+4/|x−2|=1−m, gdzie m jest parametrem m nalezy do R b) Rozwiąż to równanie w Przypadku, gdy m=−4.

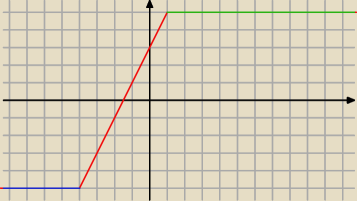
Jack: f(x) = |x+4| − |1−x| standardowo przedzialy 1^o x∊ (− ∞; − 4> f(x) = − x − 4 − (1−x) = −x − 4 − 1 +x = − 5 zatem funkcja w tym przedziale to jest po prostu prosta y = − 5. 2^o x∊(− 4; 1> f(x) = x + 4 − (1−x) = x+4 −1 +x = 2x + 3 zatem rysujemy y = 2x+3 3^o x∊(1; ∞) f(x) = x+4 − (−1+x) = x+4+1−x = 5 zatem rysujemy y = 5.