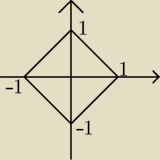
Najmniejsza i największa wartość funkcji Stokrotka: Witam wszystkich, mam problem z zadaniem na najmniejszą i największą wartość funkcji y =2x² +4xy−y² na obszarze zadanym warunkami: −1≤x≤1 −1≤y≤1. Pochodne to df/dx = 4(x+y) , df/dy = 4x−2y i nie za bardzo wiem co dalej. Pochodne się zerują w punkcie (0,0)

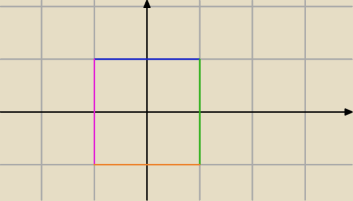
ICSP: Po pierwsze twój obszar wygląda inaczej. Teraz : 1^o Liczysz wartość funkcji w punkcie (0 , 0) 2^o Badasz ekstrema na brzegu odpowiednio go parametryzując, dla przykładu zielony odcinek mozesz sparaametryzować : I₁ = (x,y) = (1 , t) gdzie t ∊ [−1 , 1]

Stokrotka: No fakt, czy muszę badać wartości w środku tego kwadratu?, czemu tylko na brzegach? Każdy odcinek mogę sobie tak zparametryzować? l1 = 2+4t−t², czyli liczę pochodną l1` = −2t+4 a to sie rowna 0 wiec t = 2 nie należy do przedziału, i robię tak dla każdej prostej?

Stokrotka: No tak, ale jestem głupia, przecież zerowanie się pochodnych w 0, to jest badanie środka, a wartość jest równa 0. Dziękuje!