Funkcja wymierna ja: Dana jest funkcja o wzorze f(x)= (x+1)²/x²−1 a) narysuj wykres funkcji g(x)=|f(x)| b) Dla jakich argumentów funkcja h(x)= 2/x+3 + x/x−1 osiąga wartości niemniejsze niż funkcja y=f(x) ? Bardzo bym prosił o wytłumaczenie

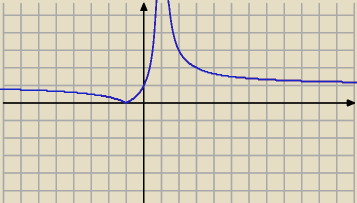
6latek: To bedzie wykres tej funkcji

	(x+1)2
f(x)=		dla x≠1 i x≠−1
	x2−1

	(x+1)2		x+1		1(x−1)+2		2
f(x)=		=		=		=		+1
	(x+1)(x−1)		x−1		x−1		x−1

Rysujesz f(x) a potem to co pod osia OX odbijasz nad os OX w b) nalezy rozwiazac nierownosc

2		x		(x+1)2
	+		≥
x+3		x−1		x2−1

Niemniejszse wedlug mnie to wiekszse badz rowne

ja: Dziękuję

ja: w b) wychodzi x∊(−3;−1) ∪ (−1;1) ∪ <5,+∞) bo x≠ −3;−1;1