Planimetria lepus: Boki trójkąta ABC mają długości: AB=8, Bc=16 oraz AC=20. Oblicz długość środkowej poprowadzonej z wierzchołka A. Jakaś wskazówka?

Jack: ktora klasa?

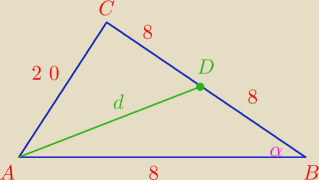
Jack: z twierdzenia cosinusow w trojkacie ABC 20² = 16² + 8² − 2*16*8 * cos α 400 = 320 − 256 cos α 256 cos α = − 80

	80		5
cos α = −		= −
	256		16

z twierdzenia cosinusow w trojkacie ABD d² = 8² + 8² − 2*8*8cosα

	5
d2 = 128 − 128 *( −		)
	16

d = ...

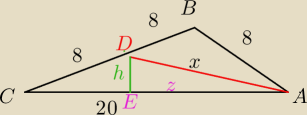
Aga1.: Oblicz pole trójkąta ABC.

	1
PACD=PABD=		P{ABC}
	2

Ze wzoru na pole trójkątaACD wylicz h. Z tw. Pitagorasa z układu wylicz x x²=z²+h² h²+(20−z)²=8²

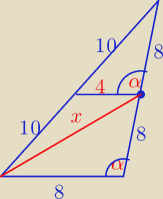
Janek191: Z tw kosinusów dla małego Δ mamy 10² = 4² + 8² − 2*4*8*cos α 100 = 16 + 64 − 64 cos α 64 cos α = − 20

	20		5
cos α = −		= −
	64		16

więc x² = 8² + 8² − 2*8*8 *cos α

	−5
x2 = 64 + 64 − 128*		= 128 + 40 = 168 = 4*42
	16

x = 2 √42 ========

lepus: Dziękuję