Geometria Nadii: Wewnątrz trójkąta ABC obrano punkt P tak, że ∡CAP=∡CBP. Uzasadnij, że ΔAPL∼ΔBPK oraz ΔAPB∼ΔKLP, gdzie punkty K i L są punktami przecięcia prostych AP i BP odpowiednio z bokami BC i AC.

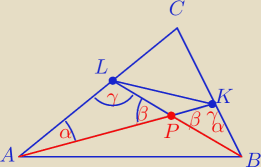
Janek191: Δ APL ∼ Δ BPK na mocy cechy podobieństwa trójkątów : kkk oraz

KP		BP
	=		i I ∡ APB I = I ∡ KPL I więc Δ ABP ∼ Δ KPL. − cecha bkb
LP		AP

Nadii : Dziękuję