Policz wszystkie rozwiązania równania z^3=1 Agaa: Policz wszystkie rozwiązania równania z³=1 Naszkicuj ich położenie na płaszczyźnie zespolonej Gaussa. Pokaż, ze stanowią one grupę przemienną ze względu na mnożenie.

Saizou : rozwiązania z³−1=0 w C to

	−i√3−1		i√3−1
μ={1,		,		}
	2		2

	i√3−1
zauważmy że		jest pierwiastkiem pierwotnym, zatem μ jest grupą cykliczną,
	2

pokażemy że jest grupą abelową: tzn. możenie jest łączne, wynika to z mnożenia liczb zespolonych

Benny: Saizou co oznacza, że coś jest grupą cykliczną?

Saizou : Czyli istnieje taki element ze zbioru, którego wielokrotności generują resztę elementów, inaczej <g>={g^o,g¹,...,gⁿ⁻¹} <g>− generator

Saizou : Jak chcesz, to możesz się odnieść w tym zadaniu bezpośrednio do grupy pierwiastków z 1

Benny: Rozumiem Gdzieś się tego używa? Do czegoś się przydaje?

Saizou : Z tego typu pytaniami nie do mnie. Wiem że coś takiego istnieje, ale nie znam zastosowania. To algebra, która nie jest moim "obiektem" westchnień. Ale sądzę że do czegoś się przydaje, w bardziej zaawansowanej algebrze.

Saizou : Jak chcesz to możesz zrobić takie zadanko? Pokaż że zbiór Z z działaniem + jest grupą cykliczną. Znajdź jego generatory.

Benny: Jak pokazać coś oczywistego? 1 będzie generatorem, bo np. 0+1=1, 1+1=2 ...

Saizou : I to jest trudność tego zadania. A jakieś inne liczby też będą generatorami ?

Benny: −1 0−1=−1, −1−1=−2 ...

Saizou : Tak a jeszcze jakieś ?

jc: Benny, gdzie używa się pierwiastków z 1? Dyskretna transformata Fouriera (złożone rachunki, przetwarzanie sygnałów, kompresja obrazów, ...)

Benny: Saizou, raczej nic już nie będzie zmieniało liczbę o 1. jc, na matmie raczej tego nie spotkam?

jc: Spotkasz na pewno, w końcu jest to bardzo ważna grupa. Pierwiastki n−tego stopnia z 1 są wierzchołkami n−kąta foremnego.

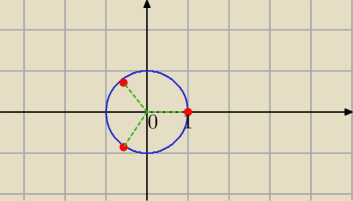
Mila: z=³√1 |1|=1 φ=0

	0+2kπ		0+2kπ
zk=1*(cos		+i sin		), k=0,1,2
	3		3

z₀=1

	2π		2π		1		√3
z1=cos		+i sin		=−		+i*
	3		3		2		2

	4π		π		1		√3
z2=cos		+i sin		=−		−i*
	3		3		2		2