Pilne Kasiulek6666: Wyznacz równanie stycznej do wykresu funkcji f w punkcie o odciętej x₀ a) f(x)=x²,x₀= −4 b)f(x)=¹_x x₀=¹₂

Janek191: a) f(x) = x² f(−4) = 16 więc f '(x) = 2 x f '( − 4) = − 8 = a y = − 8 x + b P =( − 4, 16) więc 16 = − 8*( − 4) + b ⇒ b = − 16 Odp. y = − 8 x − 16 ==============

6latek: y=f'(x₀)(x−x₀)+f(x₀) Licz i nie griluj czego nie potrafisz ? Pochodnej z x² policzyć ?

Jack: Pilnie to powinni sie uczniowie uczyc. a) f(x) = x² f(x₀) = f(−4) = (−4)² = 16 zatem chcemy styczna miec w punkcie (−4,16) f ' (x) = 2x f ' (x₀) = f ' (−4) = − 8 y = − 8 x + b u nas y = 16, x = − 4 zatem 16 = − 8 * (−4) + b 16 = 32 + b b = − 16 czyli prosta styczna to y = −8x − 16 w kartach wzorow jest na to gotowy wzor, wystarczy podstawiac.

Janek191:

	1		1
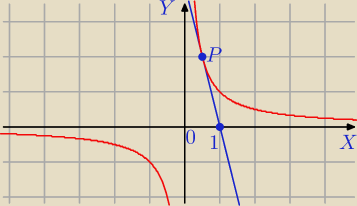
b) f(x) =		x0 =
	x		2

f(x₀) = 2

	1
f '(x) = −
	x2

	1
f '(		) = − 4 = a
	2

	1
y = − 4 x + b P = (		, 2)
	2

	1
2 = − 4*		+ b ⇒ b = 4
	2

Odp. y = − 4 x + 4 ===============