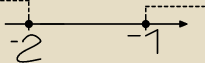
Przykładowe zadanie na nierówności wielomianowe AZ: Mógłby mi ktoś wybaczyć co robię źle? Przy każdym zadaniu wychodzi wynik "odwrotny" do prawidłowej odpowiedzi podanej z tyłu książki. x⁴ + x³ + 8x + 8 ≤ 0 x³ (x + 1) + 8 (x + 1) ≤ 0 (x³ + 8) (x + 1) ≤ 0 x³ + 2³ ≤ 0 oraz x + 1 ≥ 0 x ≤ −2 oraz x≥ −1 x∊ (−∞; −2> u <−1; ∞)

AZ: Dodam, że odpowiedź do tego zdania to wg ksiązki x∊ <−2; −1>

Jerzy: lub: x³ + 8 ≥ 0 i x + 1 ≤ 0 ( to działa ) pierwszy warunek prowadzi do sprzeczności

AZ: a jeszcze od czego zależy prowadzenie paraboli (w sensie, kiedy od góry, a kiedy od dołu)?

Jerzy: i przy okazji wybaczam

Jerzy: od znaku przy x w najwyższej potędze: gdy: + , to od góry gdy: − , to od dołu

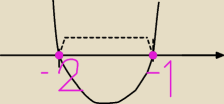
AZ: Dziękuję, czyli powinno wyjść coś takiego:

Jerzy: Tak

Jerzy: I spróbuj to: (x − 1)²(x+3)(5 − x) < 0

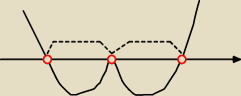
AZ: (x − 1)²(x+3)(5 − x) < 0 (x−1)² = 0 lub x+3 = 0 lub 5−x = 0 x = 1 lub x = −3 lub x = 5 x∊ (−3; 1) u (1; 5)

Jerzy: złapałeś/aś się ... jaki jest znak przy x⁴ ?

AZ: x⁴ Najwyższą potęgą jaką widzę jest (x−1)², a tam, nawet po rozwinięciu wzoru do x² − 2x + 1 jest plus. chyba że powinnam to była zrobić jakoś inaczej?

Jerzy: najwyższa potęga całego wielomianu , czyli x⁴ ( i jaki jest znak przed x⁴ ?)

AZ: Czyli parabolka będzie szła od dołu, przejdzie przez −3, odbije się od 1 i przejdzie na dół przez pięć? x∊ (−∞; −3) u (5; ∞) Sprytna pułapka, nie powiem, ale dziękuję, na pewno zapamiętam na następny raz.

Jerzy: Tak, ale odpowiedź nadal zła

Jerzy: sorry ... dobra, ale pamiętaj,że rysujemy od prawej do lewej

AZ: Hmmm, to chyba nie wiem.

Jerzy: Dobrze

AZ: Dziękuję w takim razie za pomoc i cierpliwość ze mną i życzę miłego dnia.