Płaszczyzny, poziom studiów, odległość między prostymi Bystry inaczej: Znajdź odległość między prostymi (x,y,z)=(1+2t,1+2t,1+3t), (x,y,z)=(2+3t,3+4t,4+5t) Wskazówka: Znajdź wysokość odpowiedniego równoległościanu. Na moje oko te proste nie są równoległe, jednak może ktoś wie jak to zrobić? Ja nie mam pojęcia...

Jerzy: Proste muszą być skośne ich odległość liczysz dzieląc objętość równoległościanu zbudownego na wektorch k₁,k₂ ,AB przez pole równoległoboku zbudowanego na wektorach k₁, k₂ k₁,k₂ wektory kierunkowe prostych AB A ∊ prostej k₁ , B ∊ prostej k₂

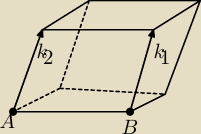
Bystry inaczej: Coś takiego? wyznaczyłem sobie punkty A=[3,3,4] i B=[5,7,9]. Dobrze myślę?

Jerzy: k₁ i k₂ sa prostymi skośnymi

Bystry inaczej: No ale to wtedy to dalej będzie równoległościan? Nie wiem jak to odpowiednio narysować, mógłbyś zademonstrować?

Mila: (x,y,z)=(1+2t,1+2t,1+3t), (x,y,z)=(2+3t,3+4t,4+5t) l₁: x=1+2t y=1+2t z=1+3t k^→=[2,2,3] wektor kierunkowy prostej l₁ P₀=(1,1,1) ∊l₁ l₂: x=2+3t y=3+4t z=4+5t u^→=[3,4,5] wektor kierunkowy prostej l₂ P₁=(2,3,4) P₁P₀^→[1,2,3] ============= 1 2 3 2 2 3 3 4 5 det(..)=2⇔proste są skośne Równanie płaszczyzny równoległej do obu prostych n^→=[2,2,3] x [3,4,5]=[−2,−1,+2] || [2,1−2] n^→=[2,1,−2] Niech P₀∊π 2*(x−1)+y−1−2(z−1)=0 2x−2+y−1−2z+2=0 π: 2x+y−2z−1=0

	|2*2+3−2*4−1|		2
d(P1(2,3,4),π)=		=
	√22+12+22		3

Bystry inaczej: Jejku Mila dzięki wielkie, ratujesz mi życie, dokładnie taki wynik miał wyjść!

Mila: Albo π₂: 2*(x−2)+y−3−2*(z−4)=0 2x−4+y−3−2z+8=0 2x+y−2z+1=0 Odległość prostych skośnych jest odległością tych dwóch płaszczyzn

	|−1−1|		2
d(π,π2)=		=
	√9		3

Posprawdzaj rachunki.

Mila: Cieszę się, dobry wynik.