Wyznacz przedziały compaq:

	1
Wyznacz przedziały w których funkcja f(x)=ln(−x+2)+		, jest malejąca oraz zbadaj czy
	4−x

posiada ekstremum lokalne właściwe.

Jerzy: 1) Wyznacz dziedzinę

	−1		1
2) f'(x) =		+		... teraz ustal , kiedy pochodna jest ujemna
	−x + 2		(4 − x)2

compaq: Więc dziedzina to: x<2 ∧ x≠4 Przedział, w którym funkcja jest malejąca x∊(−∞;2) Nie rozumiem natomiast, dlaczego mam ustalić, kiedy pochodna jest ujemna

compaq: i dlaczego mam działać na pochodnej?

Jerzy: funkcja jest malejąca w tych przedziałach, w których pochodna jest ujemna

compaq: wyszło mi, że pochodna jest ujemna dla x≤4, zgadza się?

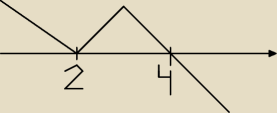
compaq: mogę prosić o sprawdzenie? f(x) maleje dla x∊(4;∞) f(x) rosnie dla x∊(−∞;2)∪(2;4)

	1
max. lok. =
	36

	−15
min. lok. =
	32

Jerzy: Zastanów się, jaka jest dziedzina tej funkcji

compaq: no tak. x≠4. wychodzi na to, ze f(x) nigdy nie maleje

Jerzy: Pytam o dziedzinę funkcji

compaq: dziedzina funkcji to x≠2 i x≠4

Jerzy: bzdura ... popatrz 11:15 wczoraj

compaq: znaczy sie x<2

Jerzy: No to badasz znak pochodnej tylko w przedziale (−∞;2)

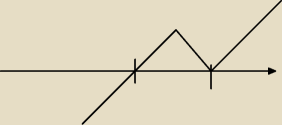
compaq: czyli f(x) maleje dla x∊ (−∞;2), zgadza sie?

compaq: w przedziale*