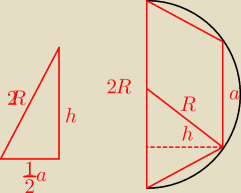
asd SASA: W półokrąg o promieniu R wpisano trapez, tak że jego dłuższa podstawa jest średnicą półokręgu, a dwa pozostałe wierzchołki należą do półokręgu. Wyznacz długość krótszej podstawy trapezu o największym polu

	1		1		1
P=		(a+2R)h=		(a+2R)√R2 −		a2
	2		2		4

	1		1
h2 +		a2=R2 ====> h=√R2 −		a2
	4		4

	1		1		1	1
P'=		√R2 −		a2 +			a
	2		4		1   2√R2 − a2   4	2

i nie wiem jak wyznaczyć a by wyszło największe pole no przyrównać do 0 by trzeba ta pochodną ale gdzieś się myle i mi nie chce wyjść

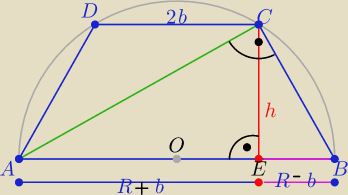myszka: |CD|=2b , b>0 trójkąt ABC jest prostokątny i |AE|= R+b , |EB|= R−b , b∊(0,R) h²=(R+b)(R−b) ⇒ h= √R²−b²

	2R+2b
P(b)=		*√R2−b2 ⇒ P(b)= (R+b)√R2−b2
	2

	b		R2−b2−Rb−b2
P'(b)= √R2−b2− (R+b)		=
	√R2−b2		√R2−b2

P^'(b)=0 −2b²−Rb+R²=0 ⇒ 2b²+Rb−R²=0 , Δ= 9R² , √Δ=3R b=...................... ................................ dokończ