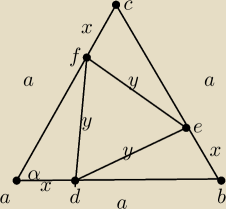
as SASA: Obwód trójkąta równobocznego ABC jest równy 3a. Punkty D,E i F należą odpowiednio do boków AB , BC , AC tego trójkąta przy czym |AD| = |BE| = |CF| = x . Wyznacz wartość x , dla której obwód trójkąta DEF jest najmniejszy α=60 Y= P{a² − 3ax + 3x²} − twierdzenie cosinusów zastanawiam sie jak mogę opisać X za pomocą a

Leszek: ΔDEF jest równoboczny o boku y z twierdzenia cosinusów y ² = a² − 3ax + 3x² obwód ΔDEF = 3y = 3*√a² − 3ax + 3x² jest to funkcja jednej zmiennej x , oblicz jej pochodną i dalej z warunków na ekstrema funkcji

agata: albo zbadaj funkcję pod pierwiastkiem−−> f. kwadratowa g(x)=3x²−3ax+a²

Leszek: TAK, o ile nie znasz rachunku różniczkowego

SASA: a faktycznie jest to funkcja jednej zmiennej przez to a sie mylę