Zadania z funkcji wykładniczej i logarytmicznej. Haylash: 1. Dana jest funkcja wykładnicza f(x)=(1/2)^x+1−2 Naszkicuj jej wykres i podaj miejsca zerowe 2. Oblicz a) log3 z 9 b)log7Pierwiastek z 7 c)log1/2 z 8 d)log 0.01 3. Oblicz: a) 9¹−log3 z 5 b) log6 z 4+2 log6 z 3 −−kreska ułamkowa−− log12 − log 6/5

Janek191:

	1
z.1 f(x) =(		) x + 1 − 2 ?
	2

Janek191: z.3 a) log₃ 9 = x ⇔ 3^x = 9 ⇔ 3^x = 3² ⇔ x = 2

	1
b) log7 √7 =		, bo 712 = √7
	2

6latek: Do zadania nr 1 . Żeby narysowac wykres jakiejkolwiek funkcji należy zrobić tabelke Taka robiles/as w szkole podstawowej i gimnazjum

Janek191: c) ... = − 3 d) ... = − 2

Janek191: z.3 a) 9^{1 − log₃ 5} = ?

Haylash: Janek191 tak, chodzi o taki właśnie zapis w pierwszym zadaniu. I czy mógłbyś podać rozwiązanie do pkt. c oraz d?

Janek191:

	1
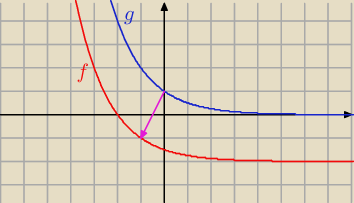
z.1 Rysujemy wykres funkcji g(x) = (		)x
	2

i przesuwamy go o wektor [ −1, −2].

Janek191:

	1		1
c) log12 8 = x ⇔ (		)x = 8 = 23 = (		)−3 ⇔x = − 3
	2		2

Janek191:

	1
log 0,01 = x ⇔ log10 0,01 = x ⇔ 10x =		⇔ x = − 2
	100

Janek191: z.3 a)

	9		9		9
91 − log3 5 =		=		=		=
	9log3 5		(32)log3 5		32 log3 5

	9		9		9
=		=		=
	3log3 52		52		25

Haylash: Dziękuje Ci ślicznie.

Janek191:

	log6 4 + 2 log6 3
b)		=
	log 12 − log 65

	log6 4 + log6 32		log6 4 + log6 9
=		=		=
	12   log   65		5   log (12* )   6

	log6 ( 4*9)		log6 36
=		=		= 2
	log 10		1

bo 6² = 36