Nierówność wielomianowa Szymon: Witam. Jak rozwiązać tą nierowność krok po kroku. z góry dziękuje (x−3)(x²−4)+3x²≤9x

Janek191: (x − 3)*( x − 2)*(x + 2) +3 x² − 9 x ≤ 0 (x −3)*(x −2)*( x + 2)+ 3x*( x − 3) ≤ 0 ( x − 3)*[( x −2)(x + 2) + 3 x] ≤ 0 (x −3)*[ x² − 4 + 3 x] ≤ 0 (x −3)*( x − 1)*(x + 4) ≤ 0 itd.

6latek : (x−3)(x²−4)+3x²−9x≤0 x³−4x−3x²+12+3x²−9x≤0 x³−13x+12≤0 Teraz x=−1 jest pierwiastkiem rownania x³−13x+12=0 wiec podziel x³−13x+12 przez x+1 i dalej szukaj pirwiastkow POtem wezyk i patrzysz gdzie ≤0

Szymon: Dziękuje za odpowiedzi ale nie rozumiem za bardzo co tutaj się stało (x −3)*(x −2)*( x + 2)+ 3x*( x − 3) ≤ 0 ( x − 3)*[( x −2)(x + 2) + 3 x] ≤ 0

Jolanta: x³−4x−3x²+12+3x²−9x≤0 x³−13x+12 ≤0 (x−1) (x²+x−12) ≤0 Δ=1²−4*(−12)=49

	−1−7
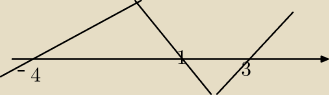
x1=		=−4
	2*1

	−1+7
x2=		=3
	2

x∊ (−∞,−4)v(1,3)

Szymon: Dziękuje Jolanta masz dobry wynik. Ale nie wiem jak z postaci x3−13x+12 ≤0 udało ci sie zrobić te 2 pierwiastki. Do schematu podstawiam 1 i wychodzi mi (x²−12x)(x−1)≤0

Janek191: Wyłączono x − 3 przed nawias

Jolanta: trzy pierwiastki x=1 znalazłam podstawiając dzielniki 12 dla x=1 1³−13*1+12=0 czyli x=1 jest pierwiastkiem a to znaczy, ze wielomian dzieli się przez x−1 podzieliłam pisemnie i otrzymałam x²+x−12