Szeregi Kuba: Zbadaj zbieżność szeregu:

	cos2n
∑n=1∞
	n(n+1)

ICSP: cos²n < 1

Krzysiek:

1		1		1
	=		−
n(n+1)		n		n+1

Leszek:

	cos2(n)		1		1
ponieważ cos2(n)<1 to ∑		≈ ∑		≈ ∑
	n(n+1)		n(n+1)		n2

i na podstawie kryterium porównawczego z szeregiem harmonicznym

	1
∑		dla k>1 podamy przez Ciebie szereg jest zbieżny
	nk

Leszek: Analogicznie zbadaj zbieżność szeregu liczbowego :

	sin2(2n+1)
∑
	√2n+1

jc: Grupujemy po 2 wyrazy i otrzymujemy szereg rozbieżny. sin² (2n−1) + sin² (2n+1) ≥ 2 sin² (π/2 − 1) > 1/2

sin2 (2n−1)		sin2 (2n+1)
	+
√2n−1		√2n+1

	sin2 (2n−1) + sin2 (2n+1)		1
>		>
	√2n+1		2 √2n+1

Leszek: dobrze jest , ale bardziej precyzyjnie będzie korzystając z kryterium porównawczego mianowicie sin²(2n+1)<1

	sin2(2n+1)		1		1		1		1
zatem ∑		≈∑		≈∑		≈		∑
	√2n+1		√2n+1		√2n		√2		√n

czyli porównujemy z szeregiem harmonicznym rzędu k = 1/2 , który jest rozbieżny (k<1) a zatem podany szereg jest rozbieżny

Leszek: Proszę zbadać zbieżność szeregu :

	√2n+1−√2n
∑
	n

n=1

jc: Leszek, jak uzasadniasz pierwsze "≈" w zadaniu z sin²(2n+1) ? Szereg faktycznie jest rozbieżny, ale to wymaga uzasadnienia.

	sin (2n+1)
A co powiesz o szeregu ∑		?
	√2n+1

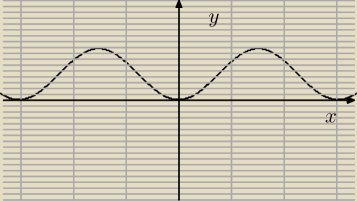
Leszek: wykres przedstawia funkcje y = sin²(x) ,to na tej podstawie sin²(2n+1)<1 dla n→∞

	sin(2n+1
natomiast −1<sin(2n+1)<1 i dlatego szereg ∑		jest przemienny
	√2n+1

jc: To, że sin² (2n+1) < 1 jest oczywiste.

	sin2 (2n+1)
Z tego faktu nie wynika rozbieżnośc szeregu ∑		.
	√2n+1

	sin2 (2n+1)		1
Napisałeś ∑		≈ ∑		.
	√2n+1		√2n+1

Co to oznacza? Jak to uzasadnić?