Udowodnij:
xcxcxc: Dany jest trójkąt prostokątny ABC, w którym |<A| = 90. Przeciwprostokatna BC ma dlugość a ,
dwusieczna AD kąta prostego ma długość d. Udowodnij, ze pole trójkata ABC jest
równe P =14 ( d2 + d √d2+2a2
4 cze 22:08
Mila:
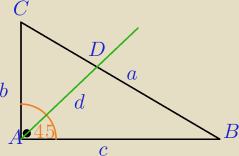
2P=b*c
8P
2=a
2d
2+4d
2*P
8P
2−4d
2P−a
2d
2=0, P>0
Δ=16d
2*(d
2+2a
2)
| | 4d2+4d*√d2+2a2 | | 4d2−4d*√d2+2a2 | |
P= |
| lub P= |
| <0 |
| | 16 | | 16 | |
================
4 cze 23:10
Jack: Milu,
Skad wiemy ze d=b*c√2/b+c?
4 cze 23:28
Mila:
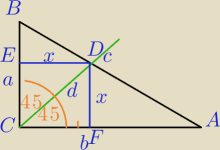
Oznaczenia standardowe.
Można to łatwo wyprowadzić.
ΔBED∼ΔBCA
x*a=b*(a−x)
x*a=b*a−b*x
x*a+x*b=a*b
x*(a+b)=a*b
| | a*b√2 | |
d= |
| jako przekątna kwadratu CFDE o boku x. |
| | a+b | |
==================================
4 cze 23:38
Jack: Ok , faktycznie latwo, dzieki
PS to w glowie wykonalas takie przeksztalcenis? ; o
4 cze 23:43
Mila:
Pamiętałam wzór (wyjątkowo), wyprowadzałam to wiele razy.
4 cze 23:56
Mila:
Masz jakiś inny pomysł na to pierwsze zadanie?
Robiłam z porównania pól.
4 cze 23:57
xcxcxc: O co chodzi w tym fragmencie?
8P2−4d2P−a2d2=0, P>0
Δ=16d2*(d2+2a2)
5 cze 15:50
Mila:
Rozwiązujesz równanie kwadratowe, niewiadomą jest P.
Oznacz sobie P=x
Masz równanie:
8x2−4d2*x−a2d2=0
a i d masz dane.
5 cze 17:57
xcxcxc: okok, dzięki wielkie

A czy jest jakieś rozwiązanie, bez wyliczania delty, bo nie robiliśmy jeszcze równań
kwadratowych?

5 cze 18:25
Mila:
Pomyślę. Na pewno jest, skoro podano takie zadanie przed równaniami kwadratowymi.
W której klasie jestś, dostosuję rozwiązanie do do materiału.
5 cze 18:41
xcxcxc: 1 liceum
5 cze 19:34
Jack: ja mialem funkcje kwadratowa przed planimetria...
hmm
| | 1 | |
miales moze wzor na pole trojkata |
| a b sin α ? |
| | 2 | |
powinienes go juz miec...
5 cze 19:59
Jack:
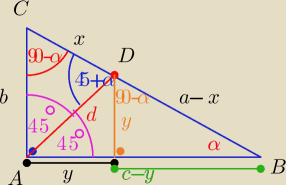
z twierdzenia o dwusiecznej (chyba jest w 1 klasie?)
cx = b(a−x)
cx = ba − bx
cx + bx = ba
x(c+b) = ba
| | ba | | a(c+b) − ab | | ac + ab − ab | | ac | |
a−x = a − |
| = |
| = |
| = |
| |
| | c+b | | c+b | | c+b | | c+b | |
y = d
√2
z pitagorasa
(c−d
√2)
2 + (d
√2)
2 = (a−x)
2
i nic z tego nie wyjdzie...
wklejam , moze sie komus przyda,
nwm jak to rozwiazac (bez znajomosci np. rownania kwadratowego czy funkcji sin/cos)
5 cze 20:19
Mila:
Jeżeli jesteś już prawie w drugiej, to miałeś wzory skróconego mnożenia i zadania z nimi
związane.
Rozwiążemy równanie bez delty. (takie zadania były w I klasie)
Zadanie dla Ciebie trudne, bo nie ma konkretnych liczb.
8x
2−4d
2*x−a
2d
2=0⇔
8x
2−4d
2*x=a
2*d
2 /:8
| | 1 | | a2d2 | |
x2− |
| d2*x= |
| uzupełnimy lewą stronę do kwadratu dwumianu |
| | 2 | | 8 | |
| | 1 | | 1 | | 1 | | a2d2 | |
(x2− |
| d2x+ |
| d4)− |
| d4= |
| ⇔ |
| | 2 | | 16 | | 16 | | 8 | |
| | 1 | | 1 | | a2d2 | |
(x− |
| d2)2= |
| d4+ |
| ⇔ |
| | 4 | | 16 | | 8 | |
| | 1 | | 1 | | 2a2d2 | |
(x− |
| d2)2= |
| d4+ |
| ⇔ |
| | 4 | | 16 | | 16 | |
| | 1 | | 1 | |
(x− |
| d2)2= |
| d2*(d2+2a2)⇔ pierwiastkujemy obustronnie |
| | 4 | | 16 | |
=====================
5 cze 20:35
xcxcxc: Dziękuje wam bardzo!
6 cze 20:05
Mila:

6 cze 20:57

 Oznaczenia standardowe.
Można to łatwo wyprowadzić.
ΔBED∼ΔBCA
Oznaczenia standardowe.
Można to łatwo wyprowadzić.
ΔBED∼ΔBCA
 A czy jest jakieś rozwiązanie, bez wyliczania delty, bo nie robiliśmy jeszcze równań
kwadratowych?
A czy jest jakieś rozwiązanie, bez wyliczania delty, bo nie robiliśmy jeszcze równań
kwadratowych?
 z twierdzenia o dwusiecznej (chyba jest w 1 klasie?)
z twierdzenia o dwusiecznej (chyba jest w 1 klasie?)
