Geometria analityczna Bystry inaczej: Znajdź rzut prostokątny punktu (2,1) na prostą 3x+4y=7

Benny: Napisz prostą prostopadłą przechodzącą przez punkt (2, 1). Punkt przecięcia prostych będzie rzutem.

Bystry inaczej: no dobra, ale jak mam wyznaczyć tą prostą? nie wiem jak mam ta prostą przedstawić w postaci parametrycznej żeby było widać wektor...

małolatka;0: Co słychać?

Benny: Chcesz to zrobić na poziomie liceum czy studia?

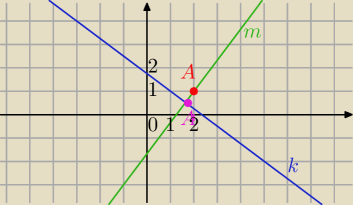
Mila: 3x+4y=7 4y=−3x+7

	−3		7
k: y=		x+
	4		4

m⊥k i A=(2,1)∊m

	4		4		5
m: y=		x+b i 1=		*2+b⇔−
	3		3		3

	4		5
m: y=		x−
	3		3

−3		7		4		5
	x+		=		x−		/*12
4		4		3		3

−9x+21=16x−20 41=25x

	41
x=
	25

	4		41		5		39
y=		*		−		=
	3		25		3		75

	41		13
A'=(		,		)
	25		25

Posprawdzaj rachunki.

Mila: II sposób: Inaczej prostopadłe ( z postaci ogólnej k: 3x+4y−7=0 m: 4x−3y+C=0 4*2−3*1+C=0 −5=C m: 4x−3y−5=0 Punkt przecięcia : 4x−3y−5=0 /*4 3x+4y−7=0 /*3 ===========

	41
x=
	25

	13
y=
	25

Bystry inaczej: dzięki Wam już rozumiem! Studia ale nie mogłem tego sam rozgryźć, a jak widać nie jest to aż takie skomplikowane

Mila: Gorzej będzie w R³.