Zadanie z planimetrii Piotr: Środkowa trójkąta prostokątnego ma długość 6cm i dzieli kąt prosty w stosunku 1:2. Oblicz obwód trójkąta.

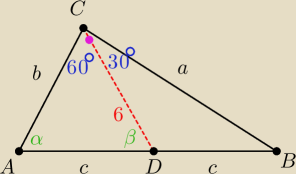
Jack: srodkowa dzieli na trojkaty o rownych polach, zatem Pole trojkata ADC = Pole trojkata DBC

1		1
	* 6 * b * sin 60 =		* 6 * a * sin 30
2		2

b sin 60 = a sin 30

	√3		1
b *		= a *
	2		2

b √3 = a z Pitagorasa w trojkacie ABC a² + b² = (2c)² (b √3)² + b² = 4c² 3b² + b² =4c² b² = c² b = c zatem trojkat ADC jest rownoramienny, a nawet wiecej − jest on rownoboczny. Wiemy to stad, ze β = 60 (bo trojkat rownoramienny), a suma katow w trojkacie to 180, zatem α = 180 − (60+60) = 60. skoro ADC jest rownoboczny, to b = c = 6 Wczesniej stwierdzilismy ze a = b√3 zatem a = 6√3 Czyli obwod : a+b+2c = 6√3 + 6 + 2*6 = 6√3 + 18 = 6(√3+3)