Proszę o pomoc Lexi:

	3 x2 − x +1
Naszkicuj wykres funkcji f (x) =		. Podaj zbiór wartości

6latek: Z wykresu odczytasz Z_w=(0,4>

6latek: nawet będzie Z_w=<0,4> bo mianownik się nie zeruje

zef: A nie przypadkiem (0;4> ?

6latek: Będzie bo funkcja nie osiągnie wartości y=0 Pomylilem z x

Mila: Niech w będzie wartością funkcji:

	3
f(x)=
	x2−x+1

Δ=1−4<0 D=R

3
	=w⇔
x2−x+1

3=w*(x²−x+1) wx²−wx+w−3=0 Badamy dla jakich w równanie ma rozwiązanie: 1)w=0 −3=0 sprzeczność 2)w≠0 Δ≥0 Δ=w²−4*w*(w−3)=w²−4w²+12w −3w²+12w≥0 i w≠0 w(−3w+12)≥0 parabola skierowana w dół w=0,w=4 w∊(0,4> Zw_f=(0,4> =====

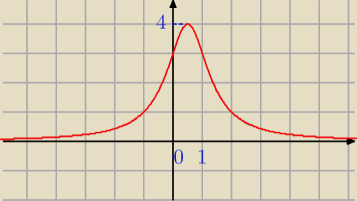
Janek191: m(x) =x² − x + 1 Δ = 1 − 4*1*1 < 0, więc x² − x + 1 > 0 dla x ∊ ℛ zatem

	3
f(x) =		> 0 dla x ∊ ℛ
	x2 − x + 1

oraz m '(x) = 2 x − 1 = 0 ⇔ x = 0,5 Funkcja m(x) osiąga minimum lokalne dla x = 0,5

	3
Wtedy funkcja f(x) osiąga maksimum lokalne ymax = f(0,5) =		=
	0,25 − 0,5 +1

	3
=		= 4
	0,75

ZWf = ( 0, 4 > ===========

jc: A mi to wygląda na funkcję z R w R². Zbiór wartości = {3} X [3/4, ∞)

Janek191: Tak dziwnie zapisane, ale pewnie 6 latek dobrze odgadł ?

6latek: Dobry wieczor MIlu

6latek: Dobry wieczor Janek191 i jc

Mila: witam wszystkich.

Janek191: I ja też

Jack: juz sie wystraszylem ze to funkcja z symbolem newtona... ; o

zef: Strach się bać

Janek191: Newtona