Benny: Dziedzina funkcji kwadratowej to R.
Jeśli mamy funkcje kwadratową w postaci kanonicznej jak powyżej tj. f(x)=a(x−p)
2+q to:
a) dla a>0 Zwf=<q; +
∞)
b) dla a<0 Zwf=(−
∞; q>
W Twoim przypadku q=0 raz a=3>0, więc Zwf=<0; +
∞)
Teraz monotoniczność, znów dwa przypadki:
a) a>0 funkcja maleje od (−
∞; p) i rośnie od (p; +
∞)
b) a<0 funkcja rośnie od (−
∞; p) i maleje od (p; +
∞)
W Twoim przypadku funkcja maleje od (−
∞; −1) i rośnie od (−1; +
∞)
Funkcja kwadratowa ma oś symetrii w x=p, czyli u Ciebie x=−1
Z wartościami największymi i najmniejszymi znów mamy dwa przypadki, możemy się odnieść do
zbioru wartości jest analogicznie
Dla:
a) a>0 mamy wartość najmniejszą w q, wartości największej nie ma, bo zbiór wartości ucieka w
nieskończoność
b) a<0 mamy wartość największa w q, wartości najmniejszej nie ma, bo zbiór wartości ucieka do
minus nieskończoności
Jak czegoś nie rozumiesz to pytaj
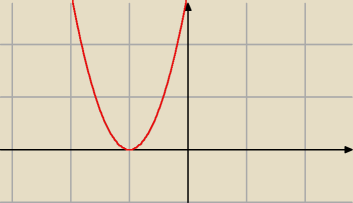D = R
Zw = <0;∞)
rownanie osi symetrii x = − 1
najmniejsza wartosc funkcji = 0