Dzidzina funkcji dwóch zmiennych drzemmajster: Witam, mam problem z dwoma przykładami treść: Znaleźć i zaznaczyć w układzie wpsółrzędnych kartezjańskich dziedzibnę funckji

	1
a)
	x*√x2 − 2y

b)p{x²+y²−4)(9−x²−y²) Myśle, że to powinno wyglądać tak, ale ręki nie dam sobei uciąć Ad a) x*√x² − 2y≠0 x≠0 ⋀ x²−2y≥0 x≠0 ⋀ −2y≥−x²

	x2
x≠0 ⋀ y≤
	2

tylko jak to zaznaczyc na wykresie ?

	x2
czyli D:((x,y)∊R2: x≠0⋀y≤		) ? <−− czy to jest prawidłowy zapis ?
	2

a w b to chyba iloczyn dwóch kół o promieniu 2 i 3, wiec żeby spełnić nierówność (to pod pierwiastkiem ≥0) dwa koła musza byc mniejsze bądź równe od zera lub większe bądź równe od zera

drzemmajster: b) √(x²+y²−4)(9−x²−y²)

Jack: a) mianownik rozny od zera zatem x * √x²−2y ≠ 0 stad x ≠ 0 ⋁ √x²−2y ≠ 0 skoro {x²−2y} ≠ 0 to x² − 2y > 0 (a nie ≥ bo zerem nie moze byc) 2y < x²

	1
y <		x2
	2

jak to zaznaczamy na wykresie?

	1
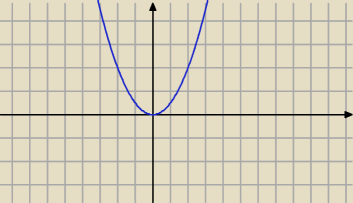
otoz rysujemy parabole y =		x2
	2

a nastepnie zaznaczamy wszystko oprocz tego co jest w srodku.

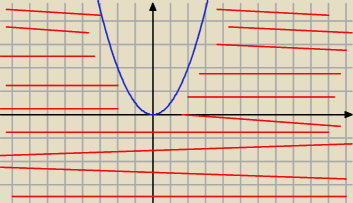
Jack: te czerwone kreski to zamalowanie.

drzemmajster: ok, dzięuję Ci bardzo pozdrawiam

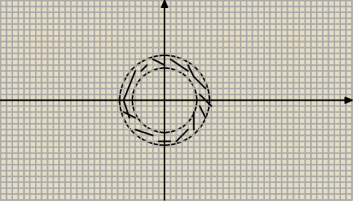
drzemmajster: a jeśli chodzi o przykąłd be to nie będzie to czasem wyglądać tak ? : (x²+y²−4)(9−x²−y²) x²+y²−4≥0 ⋀ 9−x²−y²≥0 ⋁ x²+y²−4≤0 ⋀ 9−x²−y²≤0 x²+y²≥4 ⋀ x²+y²≤9 ⋁ x²+y² ≤4 ⋁ x²+y²≥9

drzemmajster: proszę o weryfiakcje

Jack: b) to co pod pierwiastkiem ≥ 0 zatem (x²+y² − 4)(9−x²−y²)≥ 0 wyciagnijmy z drugiego minus −(x²+y²−4)(x²+y²−9) ≥ 0 // * (−1) (x²+y²−4)(x²+y²−9) ≤ 0 przyrownujemy kazde do zera i mamy x² + y² = 4 lub x²+y² = 9 Powinienes wiedziec ze jest to rownanie opisujace okrag x²+y² = 4 to okrag o srodku w punkcie(0,0) i promieniu r = 2 x²+y² = 9 to okrag o srodku w punkcie(0,0) i promieniu R = 3 Rozwiazaniem jest przestrzen miedzy tymi okregami

drzemmajster: to wiem że jest to okrąg, nawet narysowałem, czyli nie musi byc aż 2przypadków, wystarza tylko jeden po wymnożeniu przez −1 ?

Jack: tak czy owak powinny byc 2 przypadki wg mnie... u mnie (x²+y²−4)(x²+y²−9) ≤ 0 zatem x²+y² − 4≤0 /\ x²+y²−9 ≥ 0 lub x²+y² − 4≥ 0 /\ x²+y²−9 ≤ 0

drzemmajster: no to mamy tak samo tylk oja to troche inaczej zapisałem ale koncowe przyapdki są takie same dzięujęCi bardzo

Jack: