pochodna-styczna
Krzysiek:
y=x3 P=(−4;0)
Podaj wzór prostej stycznej do wykresu funkcji f i przechodzącej przez punkt P.
2 cze 13:49
Krzysiek: f(x)=x3
2 cze 13:50
Jerzy:
I gdzie problem ?
2 cze 13:51
jc: Spośród stycznych w punktach (a,a3) wybierz tą, która przechodzi przez P.
2 cze 13:56
Krzysiek: a to −4 ?
2 cze 14:06
jc: To współrzędna x−owa punktu, przez który ma przechodzic styczna.
2 cze 14:16
Jack:
f(x) = x3
f ' (x) = 3x2
prosta styczne ma wiec rownanie y = 3x + b
podstawiasz punkt P i tyle.
2 cze 14:22
Jerzy:
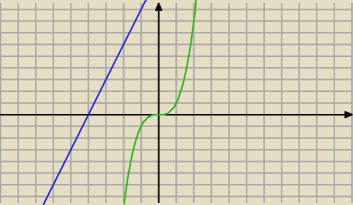
Niebieska , to Twoja syczna
Jack 
2 cze 14:27
jc: Napisz równanie stycznej w punkcie (r, r3).
Dobierz tak r, aby styczna przechodziła przez punkt P.
2 cze 14:29
Jerzy:
Musisz wyznaczyć punkt styczności x0
styczna ma równanie: y = f'(x0)(x − x0) + f(x0) , a skoro przechodzi przez punkt
P(−4,0), to:
0 = 3xo2(−4 − x0) = x03
2 cze 14:30
Jerzy:
tam ma być na końcu: 0 = 3x02(−4 − x0) + x03
2 cze 14:32
Jerzy:
Dostaniesz 2 styczne:
y = 0 lub y = 108x + 432
2 cze 14:43
Krzysiek: czyli x0 = 0 ⋁ x0 = −6
czyli y=0 ⋁ y = 108(x+6) − 63
2 cze 14:44
Krzysiek: Dzięki za pomoc
2 cze 14:44