Potrzebuję obliczeń i wyników do tych dwóch przykładów, dziękuję bardzo za pomoc
Starhin: Witam, potrzebuję rozwiązania do dwóch zadań z funkcji trygonometrycznej, a mianowicie.
| | 1 | |
a) sin ( x − pi/4 ) < − |
| |
| | 2 | |
b) cos
2 x − cos x = 0
2 cze 10:39
Metis: b) cos2x−cosx=0
cosx(cosx−1)=0
cosx=0 v cosx−1=0
cosx=0 v cosx=1
Elementarne równania.
2 cze 11:09
Starhin: i jak to będzie rozwiązanie? x = k PI? Bo równanie nie jest rozwiązane do końca

2 cze 11:13
Metis: ...
cosx=0 v cosx=1
2 cze 11:15
Starhin: Teraz mi się zgadza.
A jeśli chodzi o przykład a) ?
2 cze 11:24
Jack:
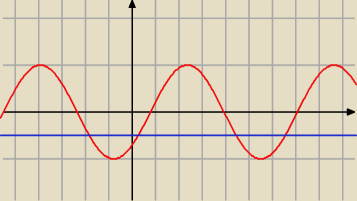
2 cze 11:25
Starhin: Nie chodzi mi o zapis graficzny tylko obliczenia

Dokładne obliczenia z przedziałem na końcu.
2 cze 15:43
Jack: 
2 cze 16:23
Jack: Nie pamietam zebym mial takie przyklady w podreczniku...
ale zrobilbym to mniej wiecej w ten sposob :
teraz odczytujesz z wykresu sinus, albo z zabawy wzorami redukcyjnymi
| | 1 | |
sin t = − |
| dla sin (30+180) oraz dla sin(360−30) |
| | 2 | |
| | 7 | | 11 | |
210 stopni to inaczej |
| π, natomiast 330 to inaczej |
| π |
| | 6 | | 6 | |
czyli
| | 7 | | 11 | |
t = |
| π + 2k π lub t = |
| π + 2kπ |
| | 6 | | 6 | |
stad
| | 7 | | 11 | |
dla t ∊ ( |
| π + 2kπ ; |
| π + 2kπ), gdzie k ∊ C |
| | 6 | | 6 | |
zatem wracam do podstawienia
| | π | | 7 | | 11 | |
(x − |
| ) ∊ ( |
| π + 2kπ ; |
| π + 2kπ) |
| | 4 | | 6 | | 6 | |
czyli
| | 7 | | π | | 11 | | π | |
x ∊ ( |
| π + |
| + 2kπ ; |
| π + |
| + 2kπ) |
| | 6 | | 4 | | 6 | | 4 | |
stad
| | 14 + 3 | | 22 + 3 | |
x ∊ ( |
| π + 2kπ ; |
| π + 2kπ) |
| | 12 | | 12 | |
| | 17 | | 25 | |
x ∊ ( |
| π + 2kπ ; |
| π + 2kπ) |
| | 12 | | 12 | |
zeby nie miec tak "brzydkich" liczb
no to wstawmy za k = − 2
| | 17 | | 17 | | 17 | | 24 | | 7 | |
wtedy |
| π + 2kπ = |
| π − 2π = |
| π − |
| π = − |
| π |
| | 12 | | 12 | | 12 | | 12 | | 12 | |
| 25 | | 25 | | 25 | | 24 | | π | |
| π + 2kπ = |
| π − 2π = |
| π − |
| π = |
| + 2kπ |
| 12 | | 12 | | 12 | | 12 | | 12 | |
zatem mozemy wlasciwie napisac
| | 7 | | π | |
x ∊ (− |
| π + 2kπ ; |
| + 2kπ) |
| | 12 | | 12 | |
ja bym to rozpisal w ten sposob, nie wiem czy to jest zgodne z matematyka (mam nadzieje ze ktos
sie pod tym postem wypowie)
jednak dla mnie to jest jak najbardziej logiczne. W kazdym razie wynik na pewno prawidlowy.
2 cze 16:40
Starhin: Z tego co się dowiedziałem dziś forma jest okrutnie zła ale wyniki się zgadzają

{17}{12} i
{1}{12}
2 cze 20:39
Jack: Podbijam aby sie dowiedziec jak inaczej rozpisac albo co poprawic w moim.
2 cze 23:44
Mila:
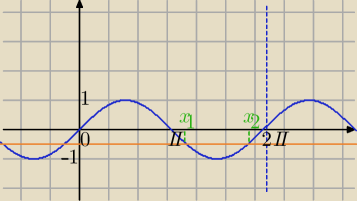
| | π | | π | |
x1+2kπ<x− |
| <x2+2kπ /+ |
| |
| | 4 | | 4 | |
| 7π | | π | | 11π | | π | |
| + |
| +2kπ<x< |
| + |
| +2kπ |
| 6 | | 4 | | 6 | | 4 | |
Wykonać dodawania i można zostawić w tej postaci.
3 cze 19:31
Jack: ok, dzieki,
podobnie do mojego...tylko krocej

3 cze 19:45


 Dokładne obliczenia z przedziałem na końcu.
Dokładne obliczenia z przedziałem na końcu.

 {17}{12} i
{1}{12}
{17}{12} i
{1}{12}

