Geometria Pomocnygość: W trójkąt równoramienny o kącie przy podstawi wpisano okrąg o promieniu 2. Oblicz pole tego trójkąta.e równym 30

Pomocnygość: Przepraszam, coś mi się poprzestawiało w treści ....o kącie przy podstawie równym 30 wpisano okrąg o promieniu R. Oblicz pole tego trójkąta

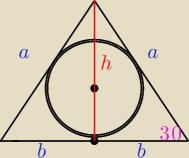Jack: jesli cala podstawe trojkata nazwiemy 2b, to wysokosc padajaca na podstawe podzieli nam podstawe na b i b. Ramie nazwalem a. z wlasnosci trojkata 30,60,90 albo z funkcji trygonometrycznych uzalezniam niewiadome od niewiadomej b.

	b√3
h =
	3

	2b√3
a =
	3

1) z Pitagorasa albo 2)Z pola trojkata : 1) jesli pitagoras to a² = h² + b² podstawiamy a i h do wzoru. itd... 2) jesli z pola trojkata

	1
Pole trojkata to		* 2b * h = bh
	2

	1
Pole tez mozna wyrazic jako		r(2a+2b) = r(a+b)
	2

zatem bh = r(a+b)

	b√3		2b√3
b*		= 2(		+b)
	3		3

b2√3		3b + 2b√3
	= 2 *		/ * 3
3		3

b²√3 = 2(3b + 2b√3) b²√3 = 6b + 4b√3 b²√3 − 4b√3 − 6b = 0 b(b√3 − 4√3 − 6) = 0 b√3 = 6+4√3

	6+4√3		6√3+12
b =		=		= 3√3 + 4
	√3		3

wiemy, ze

	b√3
h =
	3

	b√3		√3		√3
P = b * h = b *		= b2 *		= (3√3 + 4)2 *		= ...
	3		3		3

Pomocnygość: Dziękuję Ci bardzo za pomoc

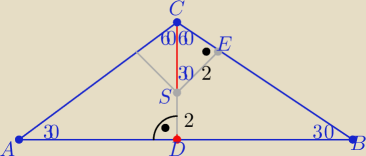myszka: To może tak: |SE|=r=2 to z trójkąta SEC o kątach 30^o, 60^o,90^o

	4√3		4√3		4√3+6
|CS|=		zatem |CD|=		+2=
	3		3		3

i z trójkąta ADC o kątach 30, 60,90

	8√3+12
|AC|= |BC|= 2|CD|=
	3

	√3
sinACB= sin120o =
	2

	1
P(ABC)=		*|AC|2*sin120o
	2

	√3		(8√3+12)2		√3
P(ABC) =		*		=		*16(2√3+3)2=
	4		9		4*9

	4√3		16
P(ABC)=		*( 12+12√3+9} =		(√3+3) [j2]
	9		3