 a)
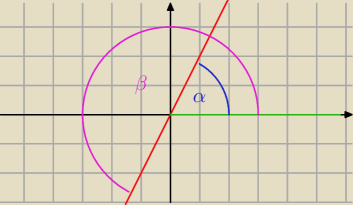
y=2x
współczynnik kierunkowy prostej jest równy tangensowi nachylenia prostej do osi Ox, zatem
tgα=2
a)
y=2x
współczynnik kierunkowy prostej jest równy tangensowi nachylenia prostej do osi Ox, zatem
tgα=2
| sinα | ||
tgα= | ||
| cosα |
| 7 | ||
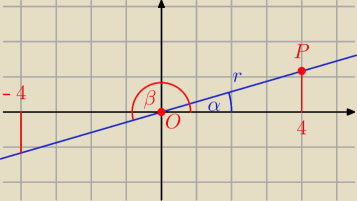
b) y = | x | |
| 24 |
| 7 | 7 | |||
Dla x = 4 jest y = | *4 = | |||
| 24 | 6 |
| 49 | 576 + 36 | 612 | ||||
r2 = x2 + y2 = 16 + | = | = | ||||
| 36 | 36 | 36 |
| y | 7 | 7 | 7 √17 | |||||
sin α = | = | : √17 = | = | |||||
| r | 6 | 6√17 | 102 |
| x | 4 | 4 √17 | ||||
cos α = | = | = | ||||
| r | √17 | 17 |
| y | 7 | |||
tg α = | = | |||
| x | 24 |
| 24 | ||
ctg α = | ||
| 7 |
| 7 | ||
Dla x = − 4 jest y = − | ||
| 6 |
| y | − 7 | 7 | 7√17 | |||||
sin β = | = | : √17 = − | = − | |||||
| r | 6 | 6√17 | 102 |
| 7√17 | ||
sin β = sin ( 180o + α) = − sin α = − | ||
| 102 |
| 4 √17 | ||
cos β = cos ( 180o + α) = − cos α = − | ||
| 17 |
| 7 | ||
tg β = tg ( 180o + α) = tg α = | ||
| 24 |
| 24 | ||
ctg β = ctg ( 180o + α) = ctg α = | ||
| 7 |