Geometria
Xx: ad. W romb o boku 10 cm i wysokości 8 cm wpisano okrąg o1:
a) Oblicz w jakiej odległości od środka boku znajduje się punkt styczności okręgu z tym bokiem.
b) Wykaż, że przez środki boków tego rombu można poprowadzić okrąg o2 i wyznacz długość
promienia tego okręgu.
ktos podpowie?

nie mam pojecia z czego ruszyc
31 maj 22:42
Mila:
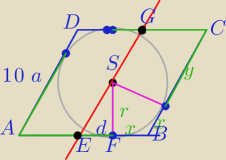
a)
|ES|=5
W ΔSFE
5
2=d
2+4
2
d=3
====
b)
wskazówka.
Narysuj za pomocą cyrkla i linijki romb.
Połącz środki boków, będziesz widział jaki to czworokąt.
|EG| to jedna z przekątnych tego czworokąta.
31 maj 23:08
Xx: Bardzo dziekuje Mila

31 maj 23:52
Mila:

1 cze 00:11
Xx: chociaz... Bo rozumiem ze chodzi o to ze kazdy bok jest w odleglosci 5 cm od srodka okregu?
Tylko daloby sie to jakos zgrabnie zapisac, czy po prostu wystarczy to napisac
1 cze 00:11
Xx: przepraszam ze zawracam ci glowe 😩
1 cze 00:12
Mila:
Tu nie mogę narysować, bo nie wyjdzie dokładnie.
Jaki czworokąt otrzymałeś łącząc środki rombu?
1 cze 00:27
Mila:
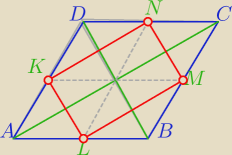
AC⊥BD
KN || AC jako odcinek łączący środki boków ΔACD, ( i KM≡LM)
MN || BD jako odcinek łączący środki boków ΔBCD, ( i KL≡MN)
⇒
KN⊥MN⇔
KLMN jest prostokątem.
Na prostokącie można opisać okrąg.
1 cze 00:39
 nie mam pojecia z czego ruszyc
nie mam pojecia z czego ruszyc
 a)
a)


 AC⊥BD
KN || AC jako odcinek łączący środki boków ΔACD, ( i KM≡LM)
MN || BD jako odcinek łączący środki boków ΔBCD, ( i KL≡MN)
⇒
KN⊥MN⇔
KLMN jest prostokątem.
Na prostokącie można opisać okrąg.
AC⊥BD
KN || AC jako odcinek łączący środki boków ΔACD, ( i KM≡LM)
MN || BD jako odcinek łączący środki boków ΔBCD, ( i KL≡MN)
⇒
KN⊥MN⇔
KLMN jest prostokątem.
Na prostokącie można opisać okrąg.