Rozwiąż angel754: a) 2x⁴ + x² − 3 =0 b) −2x² − (x−3)² ≥0 c) x³ + (2x+1)² < (x+1)³ + 12

Janek191: a) 2 x⁴ + x² − 3 = 0 t = x² ≥ 0 Mamy 2 t² + t − 3 = 0 Δ = 1 − 4*2*(−3) = 25

	− 1 − 5		− 1 + 5
t =		= − 1,5 < 0 − odpada lub t =		= 1
	4		4

więc x² = 1 x = − 1 lub x = 1 ============= b) −2 x² − ( x −3)² ≥ 0 −2 x² − ( x² − 6 x + 9) ≥ 0 −2 x² − x² + 6 x − 9 ≥ 0 −3 x² + 6 x − 9 ≥ 0 / *(−1) 3 x² − 6 x + 9 ≤ 0 / : 3 x² − 2 x + 3 ≤ 0 Δ = 4 − 4*1* 3 < 0 − brak miejsc zerowych i a = 1 > 0 , więc ramiona paraboli o równaniu y = x² − 2 x + 3 skierowane są ku górze, zatem x² − 2 x + 3 > 0 dla x ∊ ℛ Brak rozwiązań : ∅ ==================

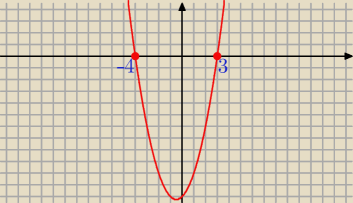
Janek191: c) x³ + (2 x + 1)² < ( x + 1)³ + 12 x³ + 4 x² + 4 x + 1 < x³ + 3 x² + 3 x + 1 + 12 / − x³ 4 x² + 4 x + 1 < 3 x² + 3 x + 13 x² + x − 12 < 0 ( x + 4)*(x − 3) < 0 x₁ = − 4 x₂ = 3 a = 1 > 0 więc x ∊ ( − 4, 3 ) ===========

Dear sir : 2x⁴+x²−3=0

wredulus_pospolitus: 2x⁴ + x² − 3 = 0 (2x² + 3)(x² − 1) = 0 ciągnij dalej