Planimetria
Mia: a) Wykaż, że długość przekątnej pięciokąta foremnego o boku 2 jest równa 1+√5.
b)Wyznacz promień r okręgu wpisanego w pięciokąt foremny o boku a i promieniu R okręgu na nim
opisanego. Odp. r=a √(5+2√5)/20 R=a √(5+√5)/10
31 maj 14:29
Mila:
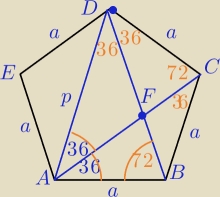
a)
Długość przekątnej.
ΔDFC− Δrównoramienny
|DF|=|DC|=a
|FB|=p−a
AF − dwusieczna kąta A w ΔDAB
p*(p−a)=a
2
p
2−pa−a
2=0, a>0
Δ=a
2+4a
2=5a
2
| | a−a√5 | | a+a√5 | |
p1= |
| <0 lub p= |
| |
| | 2 | | 2 | |
a=2
p=1+
√5
===========
31 maj 16:57
Mia: Dziękuję Mila
31 maj 18:26
Mila:
Dalej potrafisz?
31 maj 19:03
 a) Długość przekątnej.
ΔDFC− Δrównoramienny
|DF|=|DC|=a
|FB|=p−a
AF − dwusieczna kąta A w ΔDAB
a) Długość przekątnej.
ΔDFC− Δrównoramienny
|DF|=|DC|=a
|FB|=p−a
AF − dwusieczna kąta A w ΔDAB