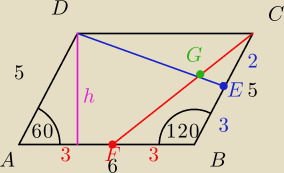
Planimetria Mia: W równoległoboku ABCD dane są: AB=6, AD=5 i ∡ABC=120. Z wierzchołków C i D poprowadzono odcinki CF i DE, których końce podzieliły boki AB i BC w stosunku odpowiednio 1:1 i 3:2. Oblicz pole czworokąta FBEG, jeśli G jest punktem przecięcia odcinków CF i DE.

Jack:

Jack: z trojkata 30,60,90

	5
h =		√3
	2

	1		5		45
Pole trapezu ADCF =		(3+6)*		√3 =		√3
	2		2		4

	5
Pole rownolegloboku ABCD = 6 *		√3 = 15√3
	2

zatem pole trojkata BCF = Pole rownolegloboku ABCD − pole trapezu ADCF =

	45		45		15
= 15√3 −		√3 = √3(15 −		) =		√3
	4		4		4

Pole czworokata FBEG to pole trojkata BCF − pole trojkata CGE wiec pozostaje nam znalezc pole tego malego trojkata. Szczerze mowiac to ja bym to narysowal w ukladzie wspolrzednym , obliczyl odleglosc punktu G od prostej BC i tak oblicyl pole trojkata, ale na pewno mozna inaczej...

jc: Czy możemy rozwiązać zadanie znając tylko pole równoległoboku = 15 √3 ? tzn. nie znając kątów i długości boków. Reszta zadania bez zmian.

prosta: pewnie można, tylko jak?

jc: CG = 1/3 CF (to oczywiście trzeba wyliczyć) CB = 2/5 CB pole CBF = 1/4 pole ABCD pole CGE = 1/3 * 2/5 pole CBF pole BEGF = pole CBF − pole CGE = 1/4 (1 − 2/15) pole ABCD = 13/60 * 15*√3

	13 * √3
=
	4

Mia: Tylko jak znaleźć pole małego trójkąta CGE?

jc: pole CGE = 1/3 * 2/5 * pole CBF Jak zmienimy długośc jednego boku, pole zmieni się proporcjonalnie. Tu zmieniamy długość jednego boku, a potem drugiego. Stąd iloczyn ułamków.

Mia: Dziękuję za pomoc

prosta:

	1
CG=		CF jak to uzasadnić? obliczyć?
	3

Kacper: Ciekawe

jc: Oczywiście z tym polem to prawda, ale moje tłumaczenie było głupie. Chodziło o to, że pozostawiamy wysokosć zmieniając długość podstawy. Jak uzyskałem 1/3? Przjąłem, że C=0 i opisałem rysunek w języku wektorów D, B. A = D + B E = 2/5 B F = 1/2 (A + B) G = t F dla pewnego t (G lezy na odcinku AF, ale A=0) G = s E + (1−s)D dla pewnego s (G leży na odcinku ED) Wszystko zapisałem za pomocą D i B Wyliczyłem t = 1/3. Algebra sama rozwiązuje takie zadania.