Granice K: lim (x→∞ ) [ −6 * √x] = −∞ , prawda ?

Jerzy: Prawda

K: Dzięki, a możesz mi sprawdzić, czy gdzieś mam poniżej błąd, czy jest to błąd w odpowiedzi (odp: ∞) lim(x→∞) [2x(√x−1 − √x+5)] =

	√x−1 + √x+5
lim(x→∞) [2x(√x−1 − √x+5)] *
	√x−1 + √x+5

	−12x
lim(x→∞)[		]
	x   1   x   5   √x( − ) + √x( + )   x   x   x   x

	−12x
lim(x→∞) [		]
	√x + √x

	−12x
lim(x→∞)[		] = lim(x→∞)[−6 * x1/2] = −∞ (a w odp jest ∞)
	2x1/2

Jerzy: Prawidłowa odp: − ∞

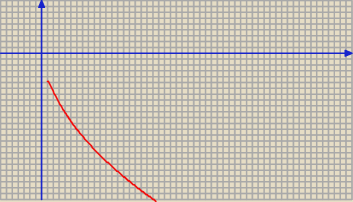Janek191: x ≥ 1

	2 x*(x −1 − (x +5)
f(x) =2x*(√x −1 − √x+5) =		=
	√x −1+ √x+5

	−12 x		− 12
=		=
	√x −1 +√x+5		√1x − 1x2 + √1x + 5x2

więc

	− 12
lim f(x) =		= − ∞
	0+

x→∞

K: Dzięki wielkie