Planimetria Mia: Dłuższa podstawa trapezu równoramiennego ma długość 4√2 , a proste zawierające ramiona trapezu przecinają się pod kątem prostym. Oblicz promień okregu opisanego na tym trapezie, wiedząc, że jest on równy długości krótszej podstawy.

Mila: Masz odpowiedź do zadania?

Mila: |SA|=2√2

d		√2
	=2R=2b⇔d=2b*sin(45)=2b*		=b√2
sin(45)		2

h=(a−b):2

	(4√2−b)
h=
	2

	a+b
|EB|=
	2

d²=h²+|EB|²

	4√2−b		4√2+b
(b√2)2=(		)2+(		)2
	2		2

	32−8b√2+b2+32+8√2b+b2
2b2=
	4

8b²64+2b² 6b²=64

	8		8√6
b=		=
	√6		6

	4√6
R=b=
	3

===============

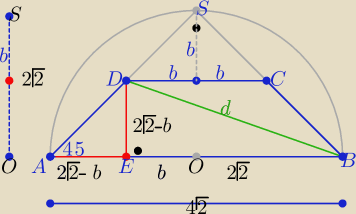
myszka: Sposób taki sam Proponuję wprowadzić "przyjazne " oznaczenia ( łatwiej się liczy |DC|=R= 2b , |DE|=2√2−b i |EB|=2√2+b . b∊(0, 2√2) z tw. sinusów w trójkącie ABD

d
	= 2R= 4b ⇒ d= 2b√2 to d2= 8b2
sin45o

z tw. Pitagorasa w ΔDEB: (2√2−b)²+ (2√2+b)²= 8b² ⇒ 8+b²+8+b²= 8b² ⇒ 6b²=16

	4		2√6
to b=		=
	√6		3

	4√6
R= 2b=
	3

=================

....: Mia i tak nie czyta tego. Wrzuca , bo ma zadanie domowe. Niestety nie możemy jej napisać rozwiązania w zeszycie. Teleportacja by się przydała.

Mia: Odpowiedź (4√6)/3

Stary: a = 4√2

	r		4
Z twierdzenia sinusow w trójkącie ABC:		=
	sin45		sin120